Хелпикс

Главная

Контакты

Случайная статья



Учитывая, что Р[(АС)(ВС)] = Р(АВС), окончательно получим P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒


#77

По условию, наступление события 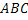 необходимо влечет наступление события 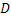, следовательно (см. задачу 48), 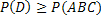. Таким образом, если будет доказано неравенство  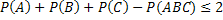(*), то будет справедливо и неравенство, указанное в условии задачи.

Докажем неравенство (*). Воспользуемся тождествами:

      (**)

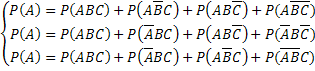Из трех событий 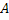, , 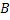 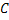можно составить следующую полную группу «сложных событий», состоящих из появлений и непоявлений рассматриваемых трех событий:

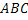 -появились все три события,

, ,

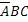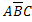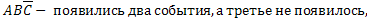
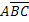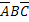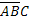, ,  – появилось одно событие, а два других не появились,

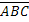 – не появились все три события.

Сумма вероятностей событий, образующих полную группу, равна единице, поэтому

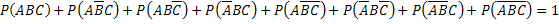
Отсюда

. (***)

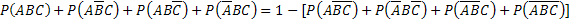Подставив (**) в (*) и используя (***), после упрощений получим

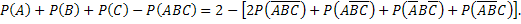
Учитывая, что каждое слагаемое в квадратной скобке неотрицательно, окончательно получим

.

 

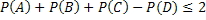#78

Вывести теорему сложения вероятностей для трех совместных событий:

 P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).

Предполагается, что для двух совместных событий теорема сложения уже доказана:

P(A1 + A2) = P(A1) + P(A2) – P(A1A2).

Решение.

 Сведем сумму трех событий к сумме двух событий: А + В + С = (А + В) + С.

Воспользуемся теоремой сложения вероятностей двух событий:

Р(А + В + С) = Р[(А + В) + С] = Р(А + В) + Р(С) - Р[(А + В)*С] = Р(А + В) + Р(С) - Р[(А*С) + (В*С)]

Применим теорему сложения вероятностей двух совместных событий дважды (для событий А и В, а также для событий АС и ВС):

Р(А + В + С) = Р(А) + Р(В) – Р(АВ) + Р(С) - {Р(АС) + Р(ВС) – Р[(АС)(ВС)]}.

Учитывая, что Р[(АС)(ВС)] = Р(АВС), окончательно получим P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).


⇐ Предыдущая123Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.