
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение задания из второй части ОГЭ модуля «Геометрия»
Тема площадь плоских фигур. (см. ссылку :https://www.youtube.com/watch?v=jCtM27FFZ9I) Ребята, знание геометрии необходимо в различных областях человеческой деятельности. Формулы площадей плоских фигур нам приходится повторять на протяжении всей жизни.
I задание: В трапеции ABCD известно, что AD = 4, BC = 2, а её площадь равна 60. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение: Проведём высоту Средняя линия равна полусумме
оснований: Площадь трапеции равна произведению по- лусуммы оснований на высоту:
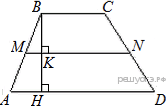
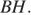
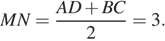
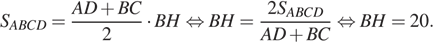
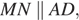
Поскольку отрезки
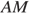
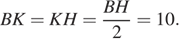 и
и 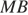 равны,
равны,
— средняя линия, поэтому по теореме Фаллеса получаем,
что 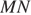


Найдём площадь трапеции
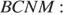
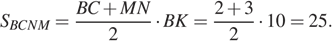
Ответ: 25.
II задание: В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
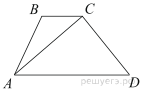
Решение: Пусть длина высоты трапеции равна 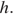 Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
Площадь трапеции можно найти как произведение полусуммы оснований на высоту: 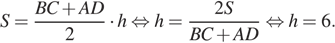
Высота трапеции также является высотой треугольника 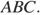 Найдём площадь треугольника
Найдём площадь треугольника 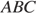 как полупроизведение основания на высоту:
как полупроизведение основания на высоту:
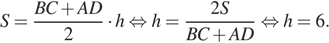
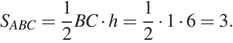
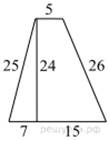
II I задачаНайдите площадь трапеции, изображённой на рисунке.
Решение: Площадь трапеции вычисляется по формуле 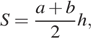 где a и b основания, а
где a и b основания, а 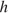 — высота трапеции.
— высота трапеции.
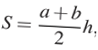


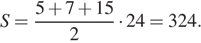
Решение задания из второй части ОГЭ модуля «Геометрия»
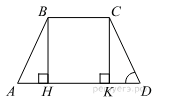
В трапеции ABCD основание AD вдвое больше основанияВСи вдвое больше боковой стороныCD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
Решение:
Опустим перпендикуляр ВН и СК на большее основание АD. По условию <АDС=600 тогда <DСК=900-600 =300 . Катет, лежащий напротив в угла в 300. Равен половине гипотенузы, тогда К=СD/2. Так как АD=2С по условию, а НК=ВС=СD, то АН= СD/2. Треугольники АВН и DСК равны по двум катетам, таким образом, трапеция АВСD- равнобедренная. Таким
образом, АВ=2, АD=4, ВН= 3. Площадь трапеции равна полусумме оснований на высоту, имеем:
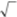

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|