
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 2. Пример 4. Пример 5. II способ.
Пример 2
Вычислить площадь фигуры, ограниченной линиями 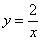 ,
, 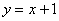 ,
, 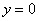 ,
, 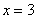 .
.
Решение: Сначала выполним чертеж:
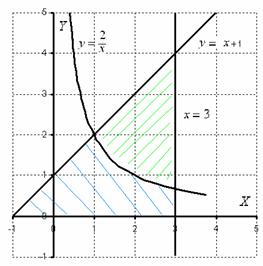
Фигура, площадь которой нам нужно найти, заштрихована синим цветом (внимательно смотрите на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована зеленым цветом!
Этот пример еще полезен и тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:
1) На отрезке 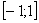 над осью
над осью  расположен график прямой
расположен график прямой 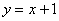 ;
;
2) На отрезке 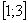 над осью
над осью 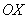 расположен график гиперболы
расположен график гиперболы 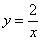 .
.
Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:
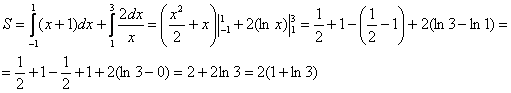
Ответ: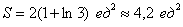
Пример 3
Вычислить площадь фигуры, ограниченной линиями: у = 4х – х2, у = 5, х = 3.
Решение:
х0 = 2, у0 = 4
Sф = SОАВД – SОСД
Sпрям. = 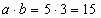 SОСД = F(3) – F(0), где F(x) первообразная для функции f(х) = 4х – х2
F(х)=
SОСД = F(3) – F(0), где F(x) первообразная для функции f(х) = 4х – х2
F(х)= 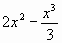 ; SОСД= ; SОСД= 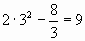 Sф = 15 – 9 = 6.
Ответ: 6.
Sф = 15 – 9 = 6.
Ответ: 6.
| 
|
Пример 4
Вычислить площадь фигуры, ограниченной линиями 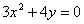 ,
, 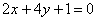
Решение:
Представим уравнения в «школьном» виде 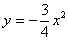 ,
, 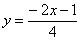 и выполним поточечный чертеж:
и выполним поточечный чертеж:

Из чертежа видно, что верхний предел у нас «хороший»: 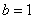 .
.
Но чему равен нижний предел?! Понятно, что это не целое число, но какое? Может быть 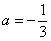 ? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что
? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что 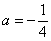 . Или корень. А если мы вообще неправильно построили график?
. Или корень. А если мы вообще неправильно построили график?
В таких случаях приходиться тратить дополнительное время и уточнять пределы интегрирования аналитически.
Найдем точки пересечения прямой 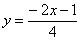 и параболы
и параболы 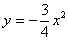 .
.
Для этого решаем уравнение:
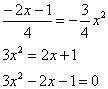
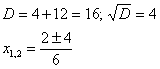
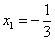 ,
, 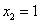
Действительно, 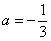 .
.
Дальнейшее решение тривиально, главное, не запутаться в подстановках и знаках, вычисления здесь не самые простые.
На отрезке 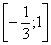
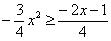 , по соответствующей формуле:
, по соответствующей формуле:
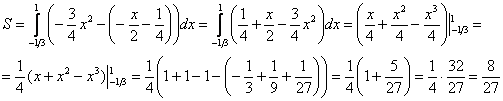
Ответ: 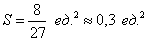
Пример 5
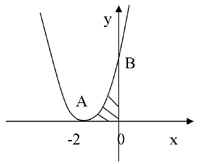
Вычислить S фигуры, ограниченной линиями у = (х + 2)2, х = 0, у = 0.
Решение:
АОВ – криволинейный треугольник или криволинейная трапеция. (рис 10.)
| S = F(0) – F(-2) =  F(x) = x2 +4x+4; F(x) =
F(x) = x2 +4x+4; F(x) = 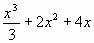 S =
S = 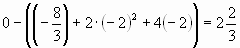
|
Ответ: 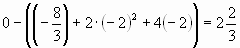
Пример 6
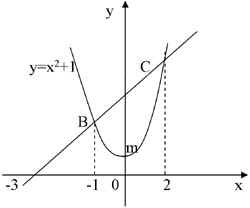
Найти S фигуры, ограниченной параболой у = х2 + 1 и прямой у = х + 3.
Решение:
Построим в одной системе координат графики данных функций.
1) у = х2 + 1, х0 = 0, у0 = 0.
| х | -3 | -2 | -1 | ||||
| у |
2) у = х + 3
3) х2 + 1 = х + 3
х1 = 1, х2 =2.
Sф = S1АВСД – S2АВmСД
Sтр.АВСД = 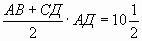 SАВmСД = F(2) – F(-1), F(x) =
SАВmСД = F(2) – F(-1), F(x) = 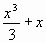 , S = 6
Sф = S1 – S2 = 4,5. , S = 6
Sф = S1 – S2 = 4,5.
| 
|
II способ.
SАВСД = F(2) – F(-1), F(x) = 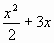 .
.
Ответ: Sф = 4,5.
Пример 7:
Найдите 3 четверти площади фигуры, ограниченной параболой, заданной уравнением у = – х2+4х-3 и осью абсцисс.
Решение:
1) хВ=2, уВ=1
2) – х2+4х-3=0 х1=3, х2=1
Функция неотрицательна на [1;3]
F(x) = 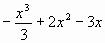 Sф = F(3) – F(1) = Sф = F(3) – F(1) = 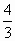 3) Умножим Sф на
3) Умножим Sф на 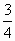 . Sиск.= . Sиск.= 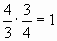 Ответ: 1
Ответ: 1
| 
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|