
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: «Производная и её геометрический смысл»
Конспект урока по алгебре в 11классе
Тема: «Производная и её геометрический смысл»
Цели урока:
Обучающие:
- повторить основные формулы раздела «Производная»
- научить учащихся решению задач на тему «Производная» из вариантов ЕГЭ (профильный уровень)
Развивающие:
- развитие познавательного интереса, логического мышления, развитие памяти, внимательности.
- воспитание интереса к обучению.
Воспитательные:
- воспитание добросовестного отношение к труду, инициативности, коммуникативности
- воспитание дисциплины и организованности
Тип урока:
- урок повторения и закрепления знаний
Структура урока:
- организационный момент;
- актуализация опорных знаний
- решение задач
- домашнее задание
Оборудование: учебник Ш.А.Алимов, Ю,М, Колягин и другие Алгебра и начала математического анализа 10-11 классы, программа презентаций MicrosoftOfficePowerPoint, презентация, компьютер, мультимедиа проектор.
План урока:
- Организационный момент
- Актуализация знаний(устный счет, повторение формул 10 мин)
- Решение задач
- Подведение итогов урока
- Домашнее задание
Ход урока:
I. Организационный момент
Учитель здоровается, знакомит с темой, целями и ходом урока.
II. Актуализация знаний
1.Вычислите производные:
а)y=x2
б)y=9x2-18x
в)y=18x5+20x2-3x+1
г)y=cos3x
д)y=5sinx
е)y=cosx+3x
ж)y=6sinx+tgx
з)y= 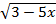
Ш. Решение задач
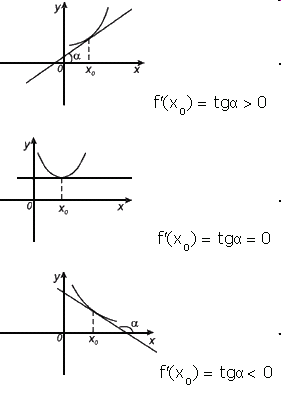
2.Повторить геометрический смысл производной (α-угол между касательной и положительным направлением оси ох ) . Индивидуальная работа по заданиям из вариантов ЕГЭ.
3.Вспомнить алгоритм составления уравнения касательной к графику функции у=f(x)
а) Обозначить абсциссу точки касания буквой α
б) Вычислить f(α)
в) Найти f’(x) и вычислитьf’(α)
г) Подставить найденные числа α,f(α),f’(α) формулу (1).
y=f(α)+f’(α)(x-α) -уравнения касательной к графику функции у=f(x)
Задания по учебнику на составление уравнения касательной №860(1,5,8).
4.Из заданных на графике точек выбрать те, в которых производная этой функции принимает:
А) положительные значения; f’(x)>0, функция возрастает
Б) отрицательные значения;f’(x)<0, функция убывает
В) значения, равные 0.f’(x)=0, max, min.
Задания по учебнику №861.
5.Задания на нахождение углового коэффициента касательной к графику функции и нахождение угла между касательной и графиком функции №858(а), 859(а).
.Домашнее задание: Пример 1
Найти площадь плоской фигуры, ограниченной линиями 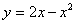 ,
, 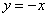 .
.
Решение: Сначала нужно выполнить чертеж. Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы 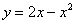 и прямой
и прямой 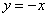 . Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:
. Это можно сделать двумя способами. Первый способ – аналитический. Решаем уравнение:
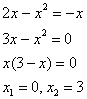
Значит, нижний предел интегрирования 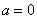 , верхний предел интегрирования
, верхний предел интегрирования 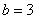 .
.
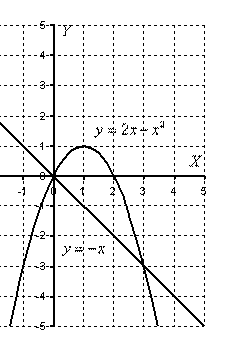
Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». Возвращаемся к нашей задаче: рациональнее сначала построить прямую и только потом параболу. Выполним чертеж:
А теперь рабочая формула: Если на отрезке 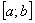 некоторая непрерывная функция
некоторая непрерывная функция 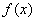 больше либо равна некоторой непрерывной функции
больше либо равна некоторой непрерывной функции 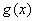 , то площадь фигуры, ограниченной графиками данных функций и прямыми
, то площадь фигуры, ограниченной графиками данных функций и прямыми 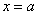 ,
, 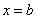 , можно найти по формуле:
, можно найти по формуле: 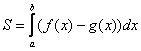
В рассматриваемом примере очевидно, что на отрезке 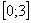 парабола располагается выше прямой, а поэтому из
парабола располагается выше прямой, а поэтому из 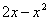 необходимо вычесть
необходимо вычесть 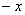
Завершение решения может выглядеть так:
Искомая фигура ограничена параболой 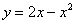 сверху и прямой
сверху и прямой 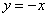 снизу.
снизу.
На отрезке 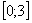
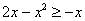 , по соответствующей формуле:
, по соответствующей формуле:
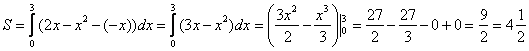
Ответ: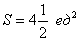
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|