Приклади використання інтеграла в фізиці, основні задачі з інтегралами в фізиці.

Інтеграл - одне з найважливіших понять математичного аналізу, яке виникає при вирішенні задач про знаходження площі під кривою, пройденого шляху при нерівномірному русі, маси неоднорідного тіла, і тому подібних, а також в завданні про відновлення функції по її похідної (невизначений інтеграл). Спрощено інтеграл можна представити як аналог суми для нескінченного числа нескінченно малих доданків. Залежно від простору, на якому задана підінтегральна функція, інтеграл може бути - подвійний, потрійний, вигнутий, поверхневий і так далі; також існують різні підходи до визначення інтеграла - розрізняють інтеграли Рімана, Лебега, Стилтьеса і інші. Символ інтеграла введений з 1675р., А питаннями інтегрального числення займаються з 1696г. Хоча інтеграл вивчають, в основному, вчені-математики, а й фізики внесли свій вклад в цю науку.

Приклади використання інтеграла в фізиці, основні задачі з інтегралами в фізиці.

1. Залежність між роботою A і силою F при переміщення матеріальної точки від значення x₁ до значення x₂ встановлюється співвідношенням:

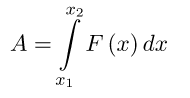
Задача:

Яку роботу треба провести, при переміщенні матеріальної точки на проміжку від 1 до 2 метрів під дією сили .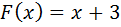

Рішення:

Шукана робота рівна:

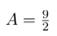
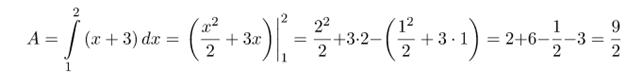
Відповідь:

2. Робота A за проміжок часу від t₁ до t₂, якщо заданий закон зміни потужності N (t), обчислюється за формулою:

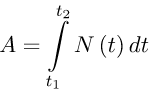
Задача: Обчисліть роботу A за проміжок часу [1; 4], якщо потужність обчислюється по формулі:

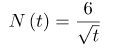
Рішення:

Шукана робота

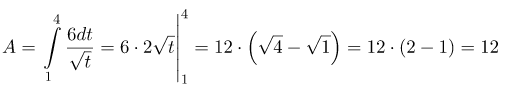
Відповідь:

3. Маса тонкого стержня
Маса 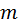тонкого стержня, якщо відома його лінійна густина 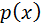обчислюється по формулі:

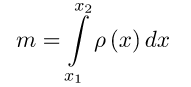
Задача: Обчисліть масу ділянки стержня від значень 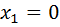до 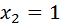, якщо його лінійна густина задається формулою .

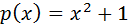Рішення:

Згідно формули маємо:

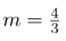
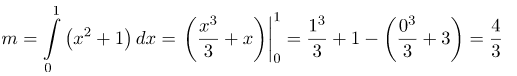
Відповідь:

4. Кількість електроенергії (електричний заряд) за проміжок часу [t₁; t₂] при відомій силі току 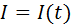обчислюється по формулі: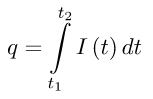

Задача: Обчисліть кількість електроенергії, я пройшла по провіднику за проміжок часу [3; 4], якщо сила току задається формулою -2t.

Рішення:

Кількість електроенергії

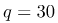Відповідь:

5. Кількість теплоти за проміжок часу

Якщо задана теплоємність 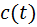, то кількість теплоти за час 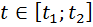, обчислюється по формулі:

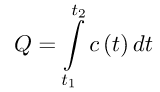
Задача:

Найти кількість теплоти. Виділеної за час 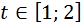, якщо теплоємність .

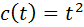Рішення:

Згідно формули маємо:

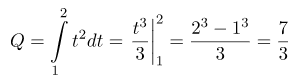
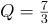Відповідь:

Джерела

1. Виноградов И. М. (гл. ред.). Интеграл // Математическая энциклопедия. — Москва., 1977. — Т. 2.

2. [Електронний ресурс] -Режим доступу: http://www.km.ru/referats/954632CE36F14A0D8BA5E72C52C20AE1

3. [Електронний ресурс] -Режим доступу: http://ru.solverbook.com/spravochnik/integraly/primenenie-integralov-v-fizike-matematike/

⇐ Предыдущая 1 23