Занятие 5. Теорема об изменении кинетического момента механической системы. Кинетический момент материальной точки и механической системы

Занятие 5

Теорема об изменении кинетического момента механической системы

Кинетический момент материальной точки и механической системы

Кинетическим моментом (моментом импульса) материальной точки относительно неподвижного центра называется вектор момента относительно этой точки вектора количества движения этой точки

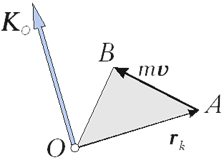
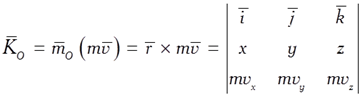
Правила определения этого вектора такие же, как и для вектора момента силы, который определялся в статике.

При решении задач вместо этого вектора часто используется скалярная величина – кинетический момент относительно оси: момент проекции вектора количества движения в плоскость, перпендикулярную оси, относительно точки пересечения оси и вспомогательной плоскости.

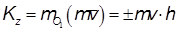
Кинетический момент относительно оси равен нулю, если вектор скорости точки лежит в одной плоскости с осью.

Часто требуется определить кинетический момент точки, совершающей сложное движение. В этом случае удобно определять момент для каждой составляющей вектора скорости

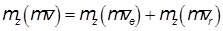
При определении кинетического момента переносной скорости следует помнить, что при переносном вращательном движении вектор скорости направлен перпендикулярно отрезку, соединяющему точку и ось вращения, поэтому

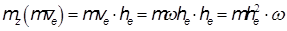В этой формуле - расстояние от точки до оси вращения. Знак кинетического момента точки в переносном движении совпадает со знаком угловой скорости.

Момент относительной скорости определяется плечом этой скорости относительно оси вращения

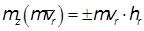
Кинетический момент твердого тела относительно неподвижной оси определяется осевым моментом инерции и угловой скоростью вращения тела

12 Следующая ⇒