
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
Рациональные и иррациональные числа, взятые в совокупности, называются действительными или вещественными.
Множество R всех действительных чисел состоит из множества всевозможных десятичных дробей (конечных, бесконечных периодических и бесконечных непериодических).
Итак, под числовой системой будем понимать то или иное множество чисел, рассмотренное вместе с операциями, которые над ними выполняются.
Каждая числовая система предназначена для решения определенного типа задач.
КОМПЛЕКСНЫЕ ЧИСЛА
Решение многих задач сводится к решению алгебраических уравнений.
Рациональные и иррациональные числа образуют множество действительных чисел. Однако, действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, уравнение
х2 + 1 = 0
не имеет действительных корней. Поэтому приходится расширять множество действительных чисел до нового множества, такого, чтобы в этом множестве уравнения вида х2 + а2 = 0 имели решения.
Корень уравнения х2 + 1 = 0 или х2 = -1 называется мнимой единицейи обозначается буквой i. Таким образом, символ i удовлетворяет условию
i2 = -1
Комплексным числом называется выражение вида a + bi , где a и b- действительные числа, i -мнимая единица. Число a называетсядействительной частью комплексного числа, а число bi - мнимой частью. Комплексное число обозначается буквой z. Запись комплексного числа в виде
z = a + bi
называется алгебраической формой записи комплексного числа.
Комплексное число z = 0+bi называется чисто мнимым, z = 0+bi = bi. При решении задач учитывать z = a+0i = a. Комплексное число z = 0+0i называется нулем. Комплексные числа a+bi и a-bi называются сопряженными.
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ
Суммой двух комплексных чисел z1 = a1 + b1i и z2 = a2 + b2 i
называется комплексное число
z1 + z2 = (a1+ a2) + (b1 + b2) i
Произведением двух комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число
z1 z2 = ( a1a2-b1b2 ) + ( a1b2+a2b1 ) i
Вычитаниекомплексных чисел вводится как операция, обратнаясложению.
Деление -как операция, обратная умножению .
Формулы не нуждаются в запоминании. Формулы суммы, разности, произведения комплексных чисел получаются автоматически, если выполнять соответствующие действия и заменить i2 = -1 .
При делении на комплексное число достаточно умножить числитель и знаменатель дроби на число, сопряженное знаменателю.

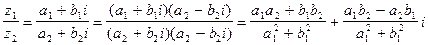
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|