
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Линейная функция
Линейная функция
• Функцию вида y = kx + b называют линейной функцией.
Буквенные множители «k» и «b» называют числовыми коэффициентами (вместо «k» и «b» могут стоять любые числа: положительные, отрицательные или дроби).
Примеры линейных функций:
1) y = 5x + 3, где k = 5, b = 3
2) y = −x + 1, где k = −1, b = 1
3) 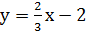 , , где k =
, , где k = 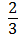 , b = - 2
, b = - 2
4) y = 0,5x, где k = 0,5, b = 0.
• Графиком линейной функции y = kx + b является прямая.
Чтобы построить график достаточно найти всего две точки, принадлежащие данной функции (значение для х берем произвольно, у высчитываем при данном значении х), построить эти точки по полученным координатам (х; у) в системе координат и через них провести прямую.
· • Если k > 0  , то график функции возрастает (наклонен вправо; движемся «в гору»)
, то график функции возрастает (наклонен вправо; движемся «в гору»)
· Если k < 0  , то график функции убывает (наклонен влево; движемся «с горы»).
, то график функции убывает (наклонен влево; движемся «с горы»).
В приведенных выше примерах: 1) функция – возрастает; 2) – убывает; 3) – возрастает
и 4) – также возрастает.
• Коэффициент b показывает ординату точки пересечения графика функции с осью ОY (т.е. график проходит через точку с координатами (0; b)).
В приведенных выше примерах: 1) функция пересекает ось ОYв точке (0; 3); 2) в точке (0; 1); 3) в точке (0; -2); 4) в точке (0; 0) – т.е. график (прямая) проходит через начало координат.
• Чтобы проверить принадлежность точки графику функции достаточно подставить координаты точки в формулу функции и выполнить арифметические расчеты:
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка не принадлежит графику функции.
• Если у линейных функций коэффициенты k равны, то графиками этих функций являются параллельные прямые.
Например графиками функций 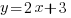 ;
; 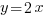 ;
; 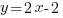 являются параллельные прямые.
являются параллельные прямые.
Обратная пропорциональность
| • Обратной пропорциональностью называется функция вида: | 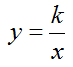
|
где k ≠ 0 и является числом.
Примеры:
1) 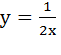 ; где k =
; где k = 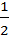 ; 2)
; 2) 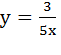 ; где k =
; где k = 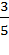 ; 3)
; 3) 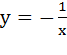 ; где k = -1.
; где k = -1.
• Областью определения функции 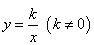 является множество всех действительных чисел, кроме x=0, т.е.
является множество всех действительных чисел, кроме x=0, т.е. 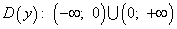
• Областью значений функции являются все числа, кроме y=0, т.е. 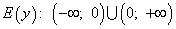
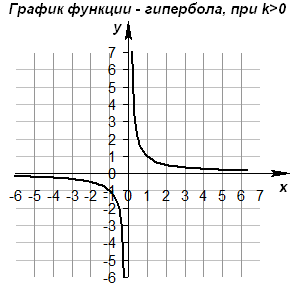
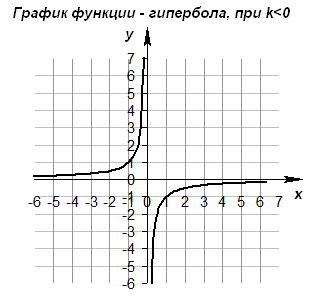
• Графиком обратной пропорциональности является гипербола.
• Если k > 0  , то ветви гиперболы расположены в I и III координатных четвертях , то ветви гиперболы расположены в I и III координатных четвертях
| 
|
• Если k < 0  , то ветви гиперболы расположены во II и IV координатных четвертях , то ветви гиперболы расположены во II и IV координатных четвертях
| 
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|