
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение.. Задача 3.. Вариант 9.. Решение.
Решение.
Рассмотрим событие A, которое заключается в том, что деталь соответствует ГОСТу. И гипотезы H1, H2, заключающиеся в том, что деталь изготовлена на первом или втором заводе соответственно.
Всего имеется 5000 деталей. Тогда вероятности того, что деталь изготовлена на первом или втором заводе соответственно, будут равны:
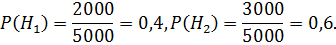
Из условия задачи вычислим условные вероятности:
– 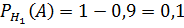 – вероятность того, что деталь, изготовленная на первом заводе, соответствует ГОСТу;
– вероятность того, что деталь, изготовленная на первом заводе, соответствует ГОСТу;
– 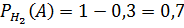 – вероятность того, что деталь, изготовленная на втором заводе, соответствует ГОСТу.
– вероятность того, что деталь, изготовленная на втором заводе, соответствует ГОСТу.
По формуле полной вероятности получаем:
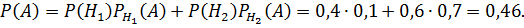
Это вероятность того, что деталь соответствует ГОСТу.
Теперь воспользуемся формулой Байеса:
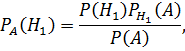
где 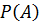 – полная вероятность.
– полная вероятность.
Получаем:
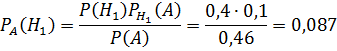
– вероятность того, что деталь изготовлена на первом заводе.
Ответ: 0,087.
Задача 3.
Вариант 9.
Вероятность возврата в срок потребительского кредита каждым из n заемщиков в среднем равна p. Найти вероятность того, что к назначенному сроку кредит вернут:
а) не менее k1 человек и не более k2 человека;
б) не менее k2 человек;
в) не более k3 человек.
Значения n = 160, k1 = 145, k2 = 155, k3 = 154, p = 0,9.
Решение.
а) Согласно интегральной теореме Лапласа, если возврата в срок потребительского кредита каждым из n заемщиков в среднем равна p, то вероятность того, что к назначенному сроку кредит вернут не менее k1 раз и не более k2 человека, приближенно определяется формулой:
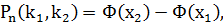
где
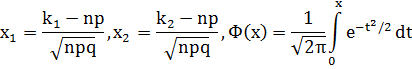
– функция Лапласа.
По условию задачи n = 160, k1 = 145, k2 = 155, p = 0,9, q = 1 – p = 0,1.
Вычислим x1 и x2:
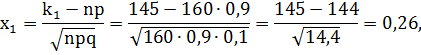

По таблице значений функции Лапласа находим:
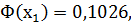
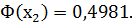
Тогда
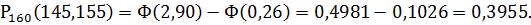
б) Требование, что кредит вернут не менее 155 человек, означает, что число вернувших кредит может быть равно 155 либо 156, либо 157, …, либо 160 (больше 160 быть не может по условию задачи). Значит, в рассматриваемом случае
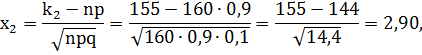
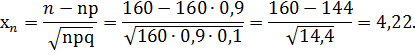
По таблице значений функции Лапласа находим:
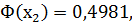

Тогда
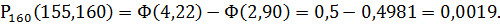
в) События «кредит вернут не менее 155 человек» и «кредит вернут не более 154 человек» противоположны, поэтому
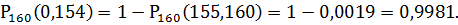
Ответ: а) 0,3955; б) 0,0019; в) 0,9981.
Задача 4.
Вариант 19.
Дискретная случайная величина задана таблицей. Найти p5, математическое ожидание, дисперсию, среднее квадратическое отклонение. Построить многоугольник распределения. Найти и изобразить графически функцию распределения.
| xi | -3 | -2 | |||
| pi | 
| 
| 
| 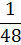
| p5 |
Решение.
Для любой дискретной случайной величины
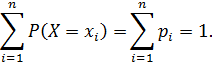
Получаем:
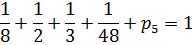
Отсюда
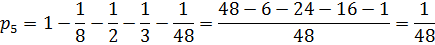
То есть закон распределения имеет вид:
| xi | -3 | -2 | |||
| pi | 
| 
| 
| 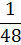
| 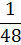
|
Математическое ожидание найдем по формуле: 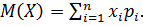
Получаем
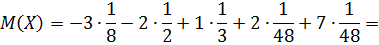
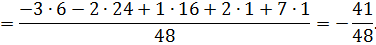
Дисперсию найдем по формуле: 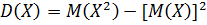 , где
, где 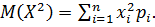 Получаем:
Получаем:
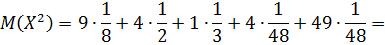
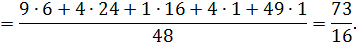
Тогда 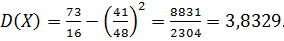
Среднее квадратическое отклонение найдем по формуле 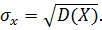
Получаем 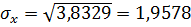 .
.
Построим многоугольник распределения.
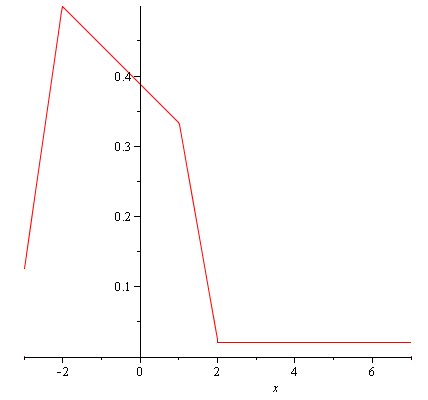
Функция распределения (интегральная функция распределения) задается формулой 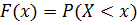 .
.
Будем задавать различные значения x и находить соответствующие значения функции.
Если 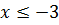 , то F(x)=0 (в том числе и при x=-3, так как F(-3)=P(X<-3)=0).
, то F(x)=0 (в том числе и при x=-3, так как F(-3)=P(X<-3)=0).
Если 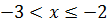 , то F(x) = P(X<-2) = P(X=-3) = 1/8.
, то F(x) = P(X<-2) = P(X=-3) = 1/8.
Если 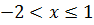 , то F(x) = P(X<1) = P(X=-3) + P(X=-2) = 1/8 + 1/2 = 5/8.
, то F(x) = P(X<1) = P(X=-3) + P(X=-2) = 1/8 + 1/2 = 5/8.
Если 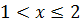 , то F(x) = P(X<2) = P(X=-3) + P(X=-2) + P(X=1) = 1/8 + 1/2 + 1/3 = 23/24.
, то F(x) = P(X<2) = P(X=-3) + P(X=-2) + P(X=1) = 1/8 + 1/2 + 1/3 = 23/24.
Если 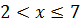 , то F(x) = P(X<7) = P(X=-3) + P(X=-2) + P(X=1) + P(X=2) = 1/8 + 1/2 + 1/3 + 1/48 = 47/48.
, то F(x) = P(X<7) = P(X=-3) + P(X=-2) + P(X=1) + P(X=2) = 1/8 + 1/2 + 1/3 + 1/48 = 47/48.
Если 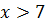 , то F(x) = 1.
, то F(x) = 1.
Получаем:
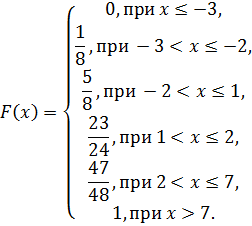
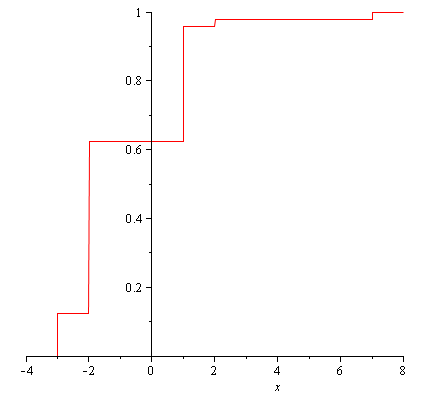
Построим график функции распределения:
Задача 5.
Вариант 10.
Непрерывная случайная величина задана функцией плотности распределения p(x):
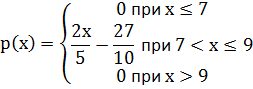
а) Найти функцию распределения F(x), построить графики функций p(x) и F(x).
б) Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение.
в) Найти вероятность того, что случайная величина примет значение на отрезке [a, b]:
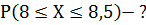
Решение.
а) Функции p(x) и F(x) связаны соотношением 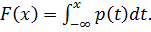
Если 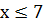 , то
, то 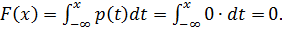
Если 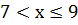 , то
, то 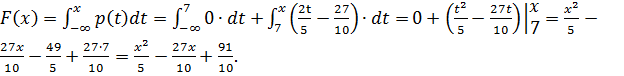
Если 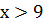 , то
, то 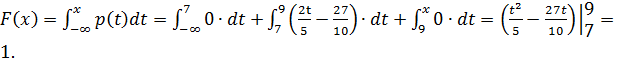
Получаем:
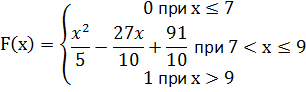
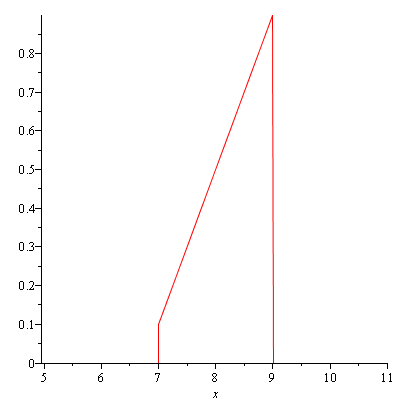
Построим график плотности распределения p(x):
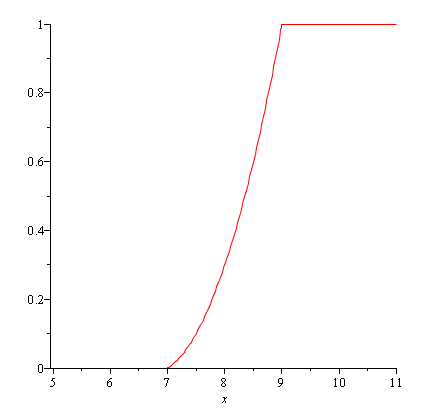
Построим график функции распределения F(x):
б) Математическое ожидание, дисперсию и среднее квадратическое отклонение найдем по формулам:
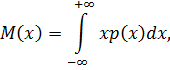
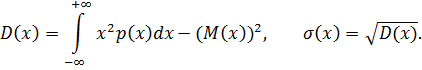
Получаем
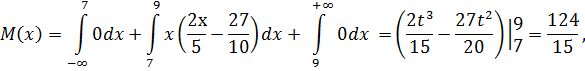
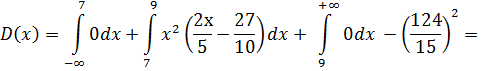
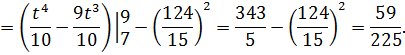

в) Вероятность того, что случайная величина примет значение на отрезке
[8, 8.5], найдем по формуле
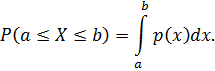
Получаем
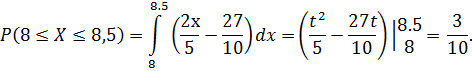
Ответ: 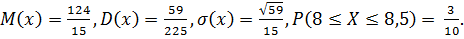
Задача 6.
Вариант 20.
Случайная величина X является нормально распределенной. Ее математическое ожидание равно M, а вероятность ее попадания в интервал (α; β) равна P. Найти среднее квадратическое отклонение σ случайной величины. Значения α = 23, M = 25, β = 27, P = 0,85.
Решение.
Вероятность попадания нормально распределенной случайной величины в заданный интервал 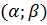 определяется через функцию Лапласа по формуле
определяется через функцию Лапласа по формуле
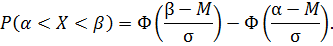
По условию задачи вероятность 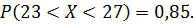
Тогда
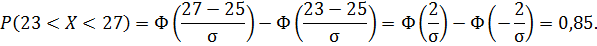
Так как функция Лапласа является нечетной функцией, для нее
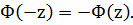
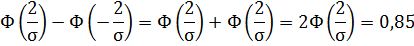
Откуда 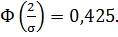
Найдем значение 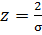 аргумента функции Лапласа. Из таблицы значений функции Лапласа получаем z=1,44. Значит,
аргумента функции Лапласа. Из таблицы значений функции Лапласа получаем z=1,44. Значит, 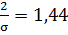 , а
, а 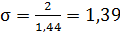 .
.
Ответ: 1,39.
Задача 7.
Вариант 11.
Для заданной выборки из генеральной совокупности случайной величины Х (n=100) необходимо:
а) определить размах варьирования случайной величины и составить вариационный ряд распределения;
б) по формуле Стерджеса определить длину интервалов и составить интервальный вариационный ряд;
в) найти выборочную среднюю 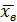 , выборочную дисперсию Dв, выборочное среднее квадратическое отклонение σв, моду Мо, медиану Ме; коэффициент вариации δв;
, выборочную дисперсию Dв, выборочное среднее квадратическое отклонение σв, моду Мо, медиану Ме; коэффициент вариации δв;
г) построить эмпирическую функцию распределения вероятностей F*(x);
д) построить гистограмму относительных частот и линию эмпирической плотности.
Решение.
а) Упорядочим значения выборки по возрастанию:
Видно, что минимальное значение = 40, максимальное = 63, значит размах варьирования равен 63 – 40 = 23.
По упорядоченным данным строим вариационный ряд распределения:
| Значения | Частоты |
б) Определяем количество интервалов по формуле Стерджеса:
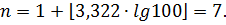
Определяем длину интервала: h = 23/7 = 3,3.
Строим интервальный вариационный ряд:
| Интервал | Частота |
| 40-43 | |
| 43-47 | |
| 47-50 | |
| 50-53 | |
| 53-56 | |
| 56-60 | |
| 60-63 |
в) Выборочное среднее
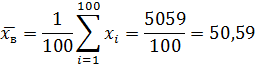
Выборочная дисперсия
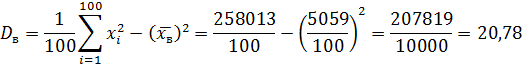
Выборочное среднее квадратическое отклонение
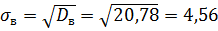
Мода Мо = 50 (это значение имеет наибольшую частоту, как видно из вариационного ряда).
Медиана Ме = 50 (делит распределение на две равные части).
Коэффициент вариации
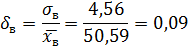
г) Эмпирическая функция распределения вероятностей F*(x) строится по вариационному ряду распределения:
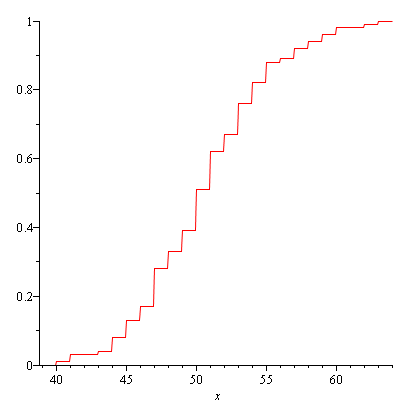
д) Гистограмма относительных частот строится по интервальному вариационному ряду:
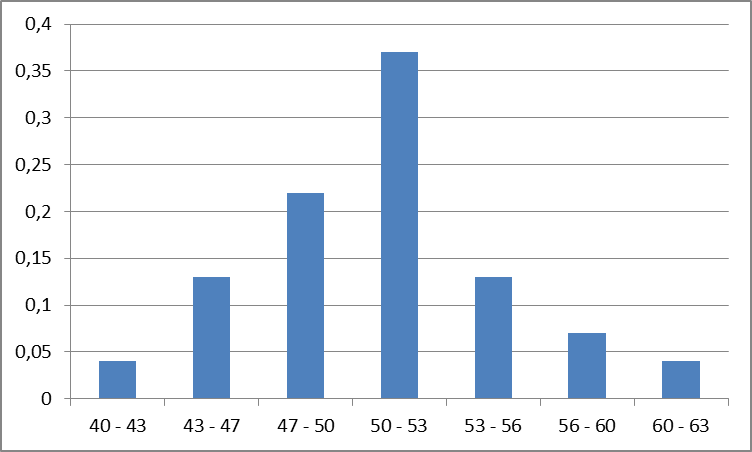
Линия эмпирической плотности:
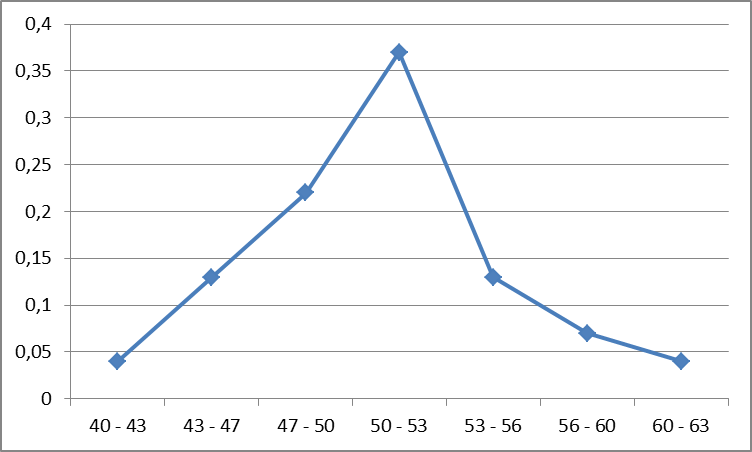
Задача 8.
Вариант 1.
Выборка X объемом N=100 измерений задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| mi | 20+(m+n) | 30-(m+n) |
Где xi - результаты измерений, mi - частоты, с которыми встречаются значения xi, 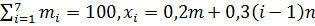 . Значения m=4, n=3. Найти распределение относительных частот, размах варьирования, полигон частот, выборочное среднее, выборочную дисперсию, выборочное среднее квадратическое отклонение, моду, медиану и коэффициент вариации.
. Значения m=4, n=3. Найти распределение относительных частот, размах варьирования, полигон частот, выборочное среднее, выборочную дисперсию, выборочное среднее квадратическое отклонение, моду, медиану и коэффициент вариации.
Решение.
Подставив значения m=4, n=3, вычислим числовые данные выборки:
| xi | x1=0,8 | x2=1,7 | x3=2,6 | x4=3,5 | x5=4,4 | x6=5,3 | x7=6,2 |
| mi |
Распределение относительных частот находим путем деления mi на 100:
| xi | x1=0,8 | x2=1,7 | x3=2,6 | x4=3,5 | x5=4,4 | x6=5,3 | x7=6,2 |
| mi | 0,05 | 0,13 | 0,27 | 0,23 | 0,19 | 0,10 | 0,03 |
Размах варьирования равен x7 - x1= 5,4.
Полигон частот:
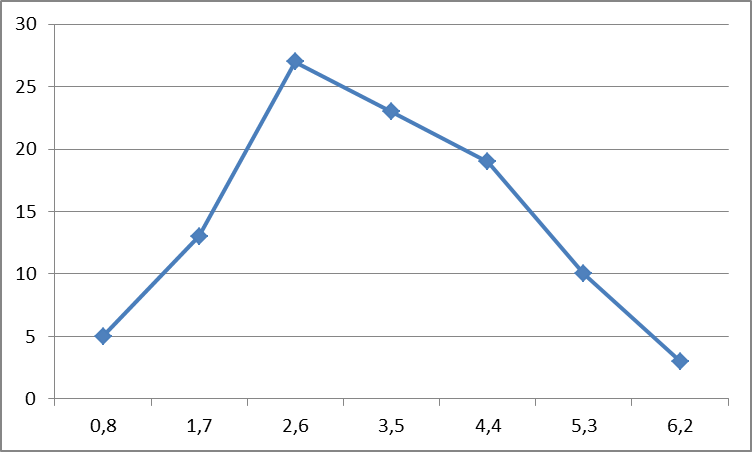
Выборочное среднее:
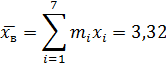
Выборочная дисперсия
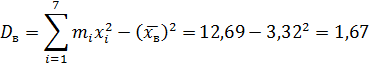
Выборочное среднее квадратическое отклонение:
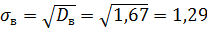
Мода: Мо = 2,6 (это значение имеет наибольшую частоту, как видно из выборки).
Медиана: Ме = 3,5 (делит выборку на две равные части).
Коэффициент вариации:

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|