Задача 1.. Вариант 8.. Решение.. Задача 2.. Вариант 18.

Задача 1.

Вариант 8.

В урне содержится K=4 черных и H=7 белых шаров. Случайным образом вынимают M=4 шаров. Найти вероятность того, что среди них имеется:

а) ровно P=2 белых шара,

б) меньше, чем P=2 белых шара,

в) хотя бы 1 белый шар.

Значения K=4, H=7, M=4 и P=2.

Решение.

а) Пусть событие A – среди вынутых шаров ровно два белых (тогда два других вынутых шара – черные). Вероятность этого события найдем, используя классическую формулу вероятности: 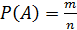, где n - число всевозможных элементарных исходов, m – число элементарных исходов, благоприятствующих данному событию. Элементарными исходами являются всевозможные сочетания:

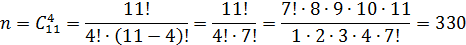
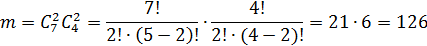
Получаем: .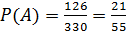

б) Пусть событие B – среди вынутых шаров меньше, чем два белых шара. Это возможно, когда вынули один белый и три черных шара или ноль белых и четыре черных шара. Поэтому

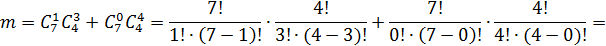
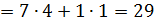
Получаем: .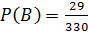

в) Пусть событие C – среди вынутых шаров хотя бы один белый шар. Перейдем к противоположному событию 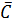- среди вынутых шаров нет ни одного белого, то есть все вынутые шары – черные. Следовательно, .

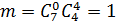Получаем: 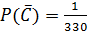, тогда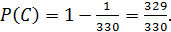

Ответ: а) 21/55, б) 29/330, в) 329/330.

Задача 2.

Вариант 18.

На автопредприятие поступили одноименные детали с двух заводов. Вероятность того, что деталь, изготовленная на первом заводе, не соответствует ГОСТу – 0,9; для второго – 0,3. Первый завод поставил 2000 деталей, второй – 3000. Сборщик взял одну деталь, которая оказалась соответствующей ГОСТу. Найти вероятность того, что эта деталь изготовлена на первом заводе.

12 Следующая ⇒