
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Распределение в анализе данных
Распределение в анализе данных
Содержание:
Дискретные величины.. 1
1. Гипергеометрическое. 2
2. Биноминальное. 3
3. Пуассоновское. 3
4. Геометрическое. 4
Непрерывные величины.. 5
1. Экспоненциальное (показательное) 5
2. Равномерное. 5
3. Нормальное (Гаусса) 6
Словарь обозначений. 7
Цитаты великих людей:
Чтобы понять какое распределение, прочитай условие задачи.
Дискретные величины
1. Гипергеометрическое
Когда применять: если достают 2 типа шаров из урны.
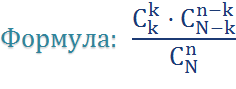
n – число вынутых шаров;
k – число вынутых шаров нужного цвета;
K – общее число шаров нужного цвета;
N – общее число шаров.
EXCEL:
p(X=k) = ГИПЕРГЕОМ.РАСП(k; n; K; N; 0)
F(X≤k) = ГИПЕРГЕОМ.РАСП(k; n; K; N; 1)
E(X): K/N*n
D(X): K/N*n 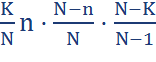
σ(X): 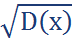
2. Биноминальное
Когда применять: дано общее количество, число подходящих испытаний и вероятность успеха.
Формула: 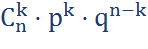
n – общее количество;
k – число подходящих;
р – вероятность успеха;
q= р-1 – вероятность провала.
EXCEL:
p(X=k) =БИНОМ.РАСП(k; n; p; 0)
р(X≤k) =БИНОМ.РАСП(k; n; p; 0)
р(a≤Х≤b) = БИНОМ.РАСП(n; p; a; b)
E(X): np
D(X): npq
σ(X): 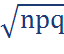
3. Пуассоновское
Когда применять: когда происходят несколько событий за какое-то время.
Формула: Р(Х=k)= 
F(X≤k): 1- 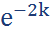 , x>0
, x>0
E(X)= D(X): λ
EXCEL: ПУАССОН.РАСП(k; λ;0/1)
4. Геометрическое
Когда применять: 1) действия повторяются до первого успеха; 2) задача на геометрию.
Формула: f(Х) qk*p,
p – вероятность успеха;
q – вероятность Неуспеха (q=1-p);
k – номер успешного испытания.
F(X): qk*p,
E(X): q/p
D(X): 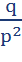
σ(X): 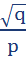
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|