
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание 13 № 517439. Задание 13 № 517446. Задание 13 № 517453. Задания Д9 C2 № 507666
Задание 13 № 517439
На ребрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём 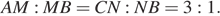 Точки P и Q — середины сторон DA и DC соответственно.
Точки P и Q — середины сторон DA и DC соответственно.
а) Доказать, что P, Q, M и N лежат в одной плоскости.
б) Найти отношение объемов многогранников, на которые плоскость PQM разбивает пирамиду.
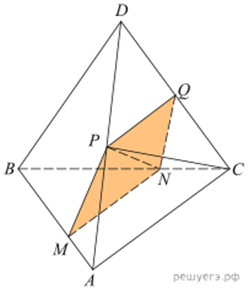 Решение.а) Треугольник ABC подобен треугольнику MBN по двум пропорциональным сторонам и углу между ними. Тогда углы BAC и BMN равны, и AC параллельно MN. Далее, PQ параллельно AC поскольку является средней линией треугольника ADC. Значит, MN параллельно PQ и поэтому P, Q, M и N лежат в одной плоскости.
Решение.а) Треугольник ABC подобен треугольнику MBN по двум пропорциональным сторонам и углу между ними. Тогда углы BAC и BMN равны, и AC параллельно MN. Далее, PQ параллельно AC поскольку является средней линией треугольника ADC. Значит, MN параллельно PQ и поэтому P, Q, M и N лежат в одной плоскости.
б) Пусть объём ABCD равен V. Пятигранник APMCQN состоит из четырёхугольной пирамиды PACNM с основанием ACNM и треугольной пирамиды PQCN с основанием QCN. Выразим их объемы через V.
Расстояние от P до плоскости BCD вдвое меньше расстояния от A до той же плоскости, при этом 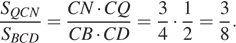 Значит,
Значит, 
Площадь треугольника MBN составляет 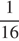 площади ABC. Значит,
площади ABC. Значит,  Расстояние от точки P до плоскости ABC вдвое меньше расстояния от D до ABC, поэтому
Расстояние от точки P до плоскости ABC вдвое меньше расстояния от D до ABC, поэтому 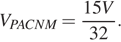
Таким образом,  то есть
то есть  Ответ: 21 : 11.
Ответ: 21 : 11.
Задание 13 № 517446
На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM : BM = CN : NB = 1 : 2. Точки P и Q — середины ребер DA и DC соответственно.
а) Докажите, что P, Q, M и N лежат в одной плоскости.
б) Найти отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.
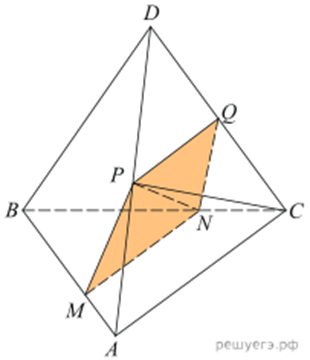 Решение.а) Треугольник ABC подобен треугольнику MBN по двум пропорциональным сторонам и углу между ними. Тогда углы BAC и BMN равны, и AC || MN. PQ || AC поскольку является средней линией треугольника ADC. Значит, MN || PQ и поэтому P, Q, M и N лежат в одной плоскости.
Решение.а) Треугольник ABC подобен треугольнику MBN по двум пропорциональным сторонам и углу между ними. Тогда углы BAC и BMN равны, и AC || MN. PQ || AC поскольку является средней линией треугольника ADC. Значит, MN || PQ и поэтому P, Q, M и N лежат в одной плоскости.
б) Пусть объём ABCD равен V. Пятигранник APMNCQ состоит из четырёхугольной пирамиды PACNM с основанием ACNM и треугольной пирамиды PQCN с основанием QCN. Выразим их объемы через V.
Расстояние от P до BCD вдвое меньше расстояния от A до BCD, а площади треугольников QCN и BCD, по теореме об отношении площадей треугольников с равным углом, относятся как 1 : 6. Значит, 
Площадь треугольника MBN составляет  площади ABC. Значит,
площади ABC. Значит, 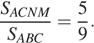 Расстояние от точки P до ABC вдвое меньше расстояния от D до ABC, поэтому
Расстояние от точки P до ABC вдвое меньше расстояния от D до ABC, поэтому 
Таким образом,  то есть
то есть 
Ответ: 13 : 23.
Задание 13 № 517453
На ребрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём 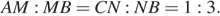 Точки P и Q — середины сторон DA и DC соответственно.
Точки P и Q — середины сторон DA и DC соответственно.
а) Доказать, что P, Q, M и N лежат в одной плоскости.
б) Найти отношение объемов многогранников, на которые плоскость PQM разбивает пирамиду.
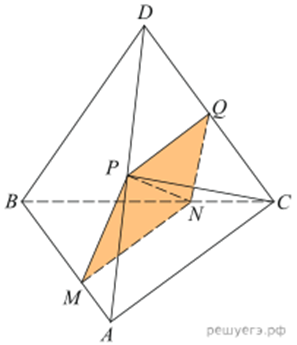 Решение.а) Треугольник ABC подобен треугольнику MBN по двум пропорциональным сторонам и углу между ними. Тогда углы BAC и BMN равны, и AC || MN. Далее, PQ || AC поскольку является средней линией треугольника ADC. Значит, MN || PQ и поэтому P, Q, M и N лежат в одной плоскости.
Решение.а) Треугольник ABC подобен треугольнику MBN по двум пропорциональным сторонам и углу между ними. Тогда углы BAC и BMN равны, и AC || MN. Далее, PQ || AC поскольку является средней линией треугольника ADC. Значит, MN || PQ и поэтому P, Q, M и N лежат в одной плоскости.
б) Пусть объём ABCD равен V. Пятигранник APMCQN состоит из четырёхугольной пирамиды PACNM с основанием ACNM и треугольной пирамиды PQCN с основанием QCN. Выразим их объемы через V.
Расстояние от P до (BCD) вдвое меньше расстояния от A до (BCD), а площади треугольников QCN и BCD относятся как 1 : 8. Значит, 
Площадь треугольника MBN составляет 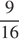 площади ABC. Значит,
площади ABC. Значит, 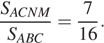 Расстояние от точки P до (ABC) вдвое меньше расстояния от D до (ABC), поэтому
Расстояние от точки P до (ABC) вдвое меньше расстояния от D до (ABC), поэтому 
Таким образом,  то есть
то есть 
Ответ: 9 : 23.
Задания Д9 C2 № 507666
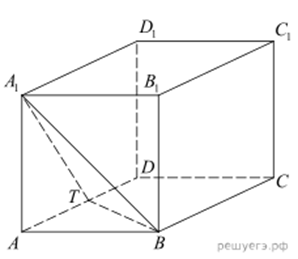 Дан куб ABCDA1B1C1D1 с ребром 1, T — середина ребра AD.
Дан куб ABCDA1B1C1D1 с ребром 1, T — середина ребра AD.
а) Докажите, что объем пирамиды 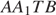 в 12 раз меньше объема куба.
в 12 раз меньше объема куба.
б) Найдите расстояние от вершины A до плоскости A1BT, где T — середина ребра AD.
Решение.а) Объем куба равен 1. Найдём объём пирамиды 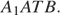 Он равен
Он равен 
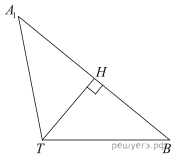 б)Пусть h — искомое расстояние. Найдём теперь объём пирамиды
б)Пусть h — искомое расстояние. Найдём теперь объём пирамиды 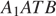 другим способом. Он равен
другим способом. Он равен  Треугольник
Треугольник  — равнобедренный, его основание
— равнобедренный, его основание 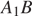 равно
равно 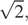 а боковые стороны равны
а боковые стороны равны 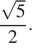 Если H — середина основания
Если H — середина основания 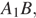 то
то 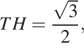 поэтому
поэтому 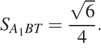 Следовательно, объём пирамиды
Следовательно, объём пирамиды 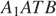 равен
равен 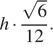 Приравняем выражения для объёма:
Приравняем выражения для объёма: 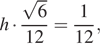 откуда
откуда 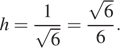 Ответ:
Ответ: 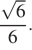
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|