
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Способы задания и свойства числовых последовательностей.
Способы задания и свойства числовых последовательностей.
Последовательность – ряд чисел
Каждое число имеет свой номер (первое, второе и т.д.)
2; 12; 22; 32…
218; 220; 218; 220;…..
1; 4; 9; 16; 25;…
а 1, а 2, а 3, …, а n ,… или (а n )
y1, y2, y3,…,yn, … или у(n).
Числовая последовательность - множество нумерованных чисел, располагаемое в порядке возрастания номеров.
Последовательность может быть конечной или бесконечной
Определение:Функцию у = f(x), x 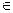 N называют функцией натурального аргумента или числовой последовательностью и обозначают: у = f(n), или у1, у2, у3..., уn или у(n) или а1 , а2,…, аn… или а(n).
N называют функцией натурального аргумента или числовой последовательностью и обозначают: у = f(n), или у1, у2, у3..., уn или у(n) или а1 , а2,…, аn… или а(n).
Способы задания последовательностей.
Ø Словесно (описание словами, без указания формулы)
Ø Аналитический способ (формулой)
Ø Рекуррентный способ задания последовательности.
Приведем три примера.
1) уn = n2 - аналитическое задание последовательности
1,4,9,16,…, n2, …, где n – номер элемента последовательности
У1 = 12 =1, У2 = 22 = 4 и т.д.
2) уn = С - последовательность С, С, С, …., С, …. . Такую последовательность называют постоянной (или стационарной).
3) Рекуррентный способ задания последовательности - указывается правило, позволяющее вычислить последующий элемент последовательности, если известны предыдущие.
а 1, = а, аn+1 = аn+ d -- арифметическая прогрессия
b 1, = b, bn+1 = bn·q --- Геометрическая прогрессия
Решение задач
№ 1. Вычислите у1, у2, у3, у4, у5 и запишите в виде ряда чисел:
А) 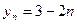
Б) 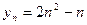
В) 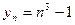
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|