
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Деление многочленов.. o. Делители многочленов. Наибольший общий делитель.
30. Деление многочленов.
Теорема 2. Пусть 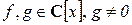 . Тогда
. Тогда 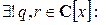
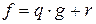 и и 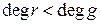 . .
| (1) |
Доказательство. Пусть 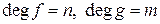 . Если
. Если 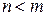 , то можно положить
, то можно положить 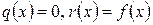 . Если
. Если  , то будем использовать тот же метод деления, что и для чисел. Пусть
, то будем использовать тот же метод деления, что и для чисел. Пусть
 и
и 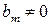 .
.
Положим 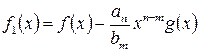 . Тогда
. Тогда 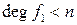 . Пусть
. Пусть 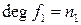 и
и  . Если
. Если 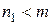 , то остановим процесс вычисления; если
, то остановим процесс вычисления; если 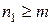 , то положим
, то положим 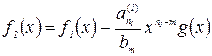 . Пусть
. Пусть  ,
,  – старший коэффициент
– старший коэффициент 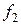 , и так далее… Так как степени многочленов
, и так далее… Так как степени многочленов 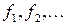 убывают, то получим
убывают, то получим 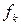 :
: 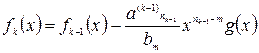 и
и 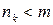 . Процесс останавливается. Суммируя полученные ранее выражения, получаем:
. Процесс останавливается. Суммируя полученные ранее выражения, получаем:
 .
.
Тогда 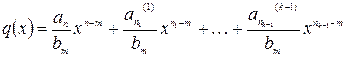 ,
,  , то есть получено требуемое представление (1).
, то есть получено требуемое представление (1).
Докажем единственность. 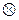 Пусть
Пусть 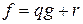 и
и  . Тогда
. Тогда 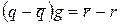 . Если
. Если  , то
, то 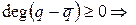 (по лемме 1)
(по лемме 1)  , a
, a  противоречие
противоречие 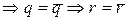 .■
.■
Определение 2. Если 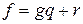 и
и 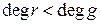 , то
, то 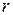 называется остатком при делении
называется остатком при делении  на
на 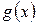 .
.
Пример. 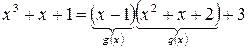 . Здесь
. Здесь 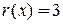 .
.
Замечание. Из указанного в теореме 2 алгоритма деления с остатком следует, что если  и
и 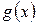 – многочлены с действительными коэффициентами, то коэффициенты всех многочленов
– многочлены с действительными коэффициентами, то коэффициенты всех многочленов  а значит и коэффициенты
а значит и коэффициенты 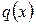 и
и 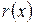 – действительные. Для целых коэффициентов это утверждение неверно.
– действительные. Для целых коэффициентов это утверждение неверно.
4o. Делители многочленов. Наибольший общий делитель.
Определение 3. Пусть 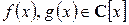 . Если
. Если 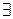
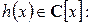
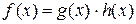 , то говорят, что
, то говорят, что  делится на
делится на 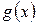 или
или 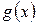 делит
делит  , и пишут
, и пишут 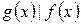 . Если
. Если 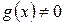 , то
, то 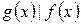 означает, что остаток от деления равен
означает, что остаток от деления равен 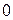 . В этом случае многочлен
. В этом случае многочлен 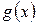 называется делителем многочлена
называется делителем многочлена  .
.
Свойства (делимости многочленов). Пусть  ,
, 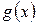 ,
, 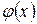 ,
, 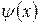 ,
, 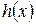 ,
, 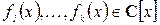 . Тогда справедливы свойства:
. Тогда справедливы свойства:
1) Если 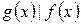 ,
, 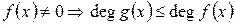 .
.
Доказательство следует из равенства 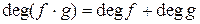 .
.
2) 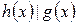 ,
, 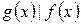

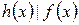 .
.
Доказательство. Так как 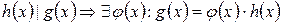 ; так как
; так как
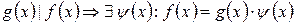 . Тогда имеем
. Тогда имеем
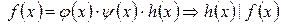 .
.
3) 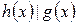 ,
, 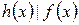

 .
.
4) 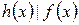

 выполняется
выполняется 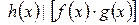 .
.
Доказательство. 
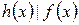

 . Тогда
. Тогда
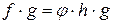 ; следовательно,
; следовательно, 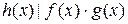 .
.
5) Если 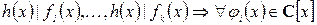 ,
, 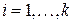 , то справедливо
, то справедливо
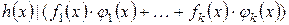 .
.
6) 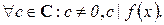
Доказательство следует из равенства 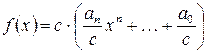 .
.
7) 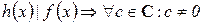 имеем
имеем  .
.
8) 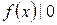 .
.
Действительно, 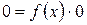 .
.
9) 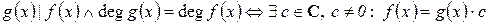 .
.
Доказательство.
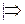
 и
и 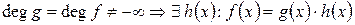 . Ho
. Ho 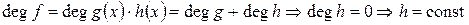 .
.

 и
и  .
.
10) 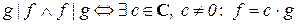 .
.
Доказательство.
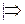 Если
Если  имеем
имеем 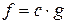 .
.
Если 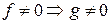 и по свойству 1 имеем
и по свойству 1 имеем 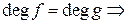 (в силу свойства 9)
(в силу свойства 9) 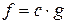 .
.
 Следует из свойства 9.
Следует из свойства 9.
11) Если  , то
, то 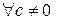 имеем
имеем 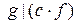 .
.
Определение 4. Многочлен 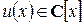 называется общим делителем
называется общим делителем  и
и  , если
, если 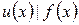 и
и 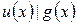 . Наибольшим общим делителем (НОД) двух многочленов
. Наибольшим общим делителем (НОД) двух многочленов  и
и 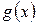 называется их делитель
называется их делитель  , который делится на любой другой их общий делитель.
, который делится на любой другой их общий делитель.
Замечание. Ненулевая постоянная является общим делителем любых двух многочленов.
Лемма 1. Если НОД двух многочленов  и
и 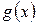 существует, то он определен с точностью до множителя
существует, то он определен с точностью до множителя  .
.
Доказательство. Пусть 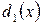 и
и 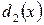 – два НОД для
– два НОД для 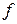 и
и 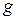
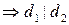 и
и 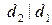
 (по свойству 10)
(по свойству 10) 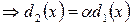 , для
, для 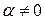 и
и 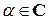 . Пусть
. Пусть 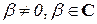 . Если
. Если 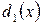 – общий делитель для
– общий делитель для  и
и 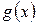 , то
, то  – тоже общий делитель. Если
– тоже общий делитель. Если  – НОД, то есть любой другой делитель делит
– НОД, то есть любой другой делитель делит  , то
, то 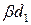 − тоже НОД.■
− тоже НОД.■
Лемма 2. Если 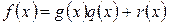 ,
, 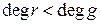 , то пары многочленов
, то пары многочленов 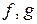 и
и 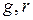 имеют одинаковые общие делители.
имеют одинаковые общие делители.
Доказательство. Пусть 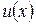 – общий делитель
– общий делитель  и
и 

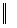 из
из 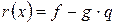 и по свойству 5
и по свойству 5 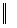
 . Аналогично, из делимости
. Аналогично, из делимости 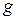 и
и 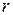 на
на 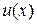

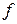 и
и 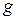 делятся на
делятся на 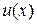 .■
.■
Лемма 3. Если  , то
, то 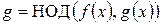 .
.
Доказательство следует из того, что 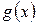 – делитель
– делитель 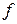 и
и 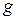 и любой делитель
и любой делитель 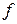 и
и 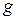 делит
делит 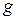 .
.
Теорема 3. Для 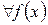 ,
, 
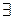 НОД(
НОД( 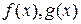 )
) 
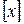 .
.
Доказательство. Рассмотрим 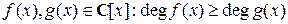 . Если
. Если  , то в силу леммы 3 и условия
, то в силу леммы 3 и условия 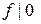 имеем
имеем 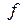 = НОД(
= НОД( 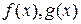 ). Если
). Если 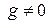 , то поделим
, то поделим 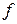 на
на 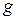 с остатком
с остатком 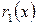 . Если
. Если 
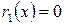 , то теорема доказана в силу леммы 3.
, то теорема доказана в силу леммы 3.
Пусть 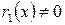 . Тогда делим
. Тогда делим 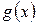 на
на 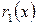 . Если остаток
. Если остаток  , то доказательство завершаем, если
, то доказательство завершаем, если 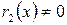 , то делим
, то делим 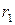 на
на 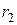 и так далее. Так как степени остатков все время уменьшаются, то процесс конечен. Таким образом, имеем следующую последовательность равенств:
и так далее. Так как степени остатков все время уменьшаются, то процесс конечен. Таким образом, имеем следующую последовательность равенств:
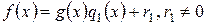 , ,
| |
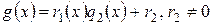 , ,
| |
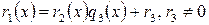 , ,
| |
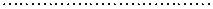
| (E) |
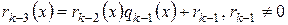 , ,
| |
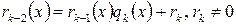 , ,
| |
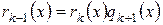 . .
|
Здесь  .
.
Из равенств ( 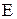 ) и леммы 2
) и леммы 2  что пары многочленов
что пары многочленов 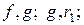
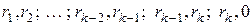 имеют общие делители
имеют общие делители  делители
делители 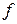 и
и 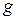 совпадают с делителями многочлена
совпадают с делителями многочлена  (по лемме 3)
(по лемме 3) 
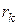 – делитель
– делитель 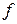 и
и 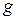 .
.
Если 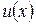 – любой другой делитель
– любой другой делитель 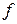 и
и 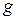
 он делитель и
он делитель и 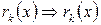 – НОД.■
– НОД.■
Замечание 1. Алгоритм построения НОД, использованный в теореме 3, называется алгоритмом Евклида или алгоритмом последовательного деления.
Замечание 2. Если 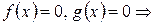
 .
.
Замечание 3. Так как НОД определен с точностью до множителя, то будем считать, что коэффициент при старшей степени равен 1.
Пример. Пусть 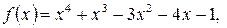
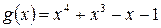 . Используем формулы (E) для построения НОД
. Используем формулы (E) для построения НОД  Тогда
Тогда 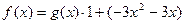 , где
, где 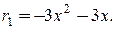 Далее удобно рассматривать
Далее удобно рассматривать 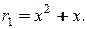 Тогда
Тогда  где
где 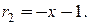 Отсюда получаем:
Отсюда получаем: 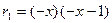 , то есть НОД
, то есть НОД 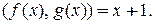
Замечание 4. При вычислении НОД результаты деления многочленов можно умножать и делить на элементы из С, что влияет лишь на множители.
Теорема 4 (теорема о разложении НОД). Пусть 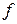 и
и  ,
, 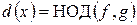 . Тогда
. Тогда 

| (2) |
При этом, если  , то
, то 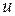 и
и 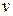 можно подобрать так, что
можно подобрать так, что  и
и 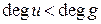 .
.
Доказательство. Если  , то по лемме 3 g(x)=
, то по лемме 3 g(x)=  и поэтому
и поэтому 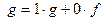 .
.
Аналогично, если 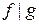 .
.
Пусть теперь 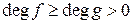 и
и 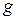 не является делителем
не является делителем 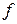 . Тогда можно считать, что
. Тогда можно считать, что  . Из предпоследнего равенства из (Е) следует, что
. Из предпоследнего равенства из (Е) следует, что
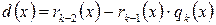 . Положим
. Положим 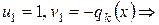
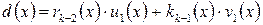 .
.
Из равенства 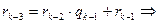

 подставляя в последнее выражение для d(x)
подставляя в последнее выражение для d(x) 
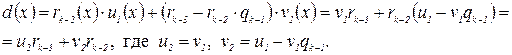
Поднимаясь дальше вверх, приходим к (2).
Докажем второе утверждение теоремы. Пусть (2) получено, но 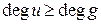 . Покажем, что (2) можно привести к виду
. Покажем, что (2) можно привести к виду 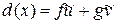 , где
, где  . Разделим
. Разделим 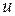 на
на 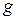 с остатком:
с остатком:  , где
, где 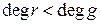 .. Подставляя это
.. Подставляя это 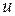 в (2), имеем:
в (2), имеем:
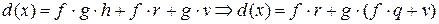 .
.
Положим 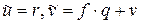 . Тогда
. Тогда 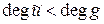 . Покажем, что
. Покажем, что  .
.  От противного, то есть пусть
От противного, то есть пусть 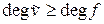 . Тогда имеем:
. Тогда имеем: 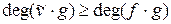 .Так как из
.Так как из 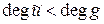 следует
следует  , то
, то  , что противоречит определению НОД.■
, что противоречит определению НОД.■
Пример. Если  ,
, 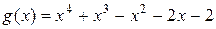 , то НОД(
, то НОД( 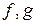 )=
)= 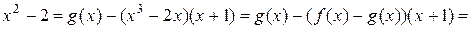
 . Следовательно,
. Следовательно,  .
.
Замечание. Аналогично вводится понятие НОД для случая многих многочленов.
5˚. Взаимно простые многочлены.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|