
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Многочлены. о. Эвристические соображения.. o. Точные определения.
§ 2. Многочлены
1о. Эвристические соображения.
В школьном курсе многочленом (полиномом) от одной переменной 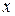 с коэффициентами из R называется выражение вида
с коэффициентами из R называется выражение вида
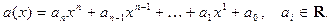
Здесь под 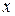 понимается некоторый символ, который может принимать любые значения из R.
понимается некоторый символ, который может принимать любые значения из R.
В дальнейшем будем рассматривать многочлены как формальные выражения. Более того, для удобства формальной записи алгебраических операций многочлены желательно рассматривать как сумму бесконечного числа слагаемых вида 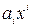 с конечным числом отличных от нуля слагаемых:
с конечным числом отличных от нуля слагаемых: 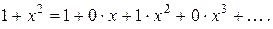 Тогда формулы для суммы и произведения многочленов примут вид:
Тогда формулы для суммы и произведения многочленов примут вид:
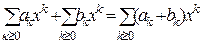 ;
;
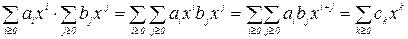 ,
,
где 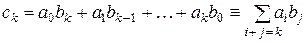 .
.
2o. Точные определения.
Определение 1. Многочленом одной переменной с коэффициентами из множества комплексных чисел С называется бесконечная последовательность 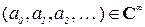 , в которой лишь конечное число элементов не равно нулю.
, в которой лишь конечное число элементов не равно нулю.
Множество многочленов с коэффициентами из С обозначается 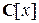 . Аналогично вводится множество
. Аналогично вводится множество 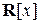 многочленов с коэффициентами из
многочленов с коэффициентами из  . Далее утверждения формулируются для многочленов из
. Далее утверждения формулируются для многочленов из 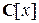 , и, если не оговорено специально, они справедливы для многочленов из
, и, если не оговорено специально, они справедливы для многочленов из 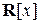 .
.
Введем операции сложения и умножения многочленов. Пусть 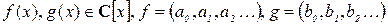 . Тогда
. Тогда
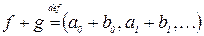 ,
, 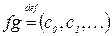 , где
, где 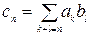 .
.
Очевидно, что 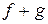 и
и  имеют лишь конечное число ненулевых элементов, то есть являются многочленами. При этом, если
имеют лишь конечное число ненулевых элементов, то есть являются многочленами. При этом, если  имеет
имеет  , а
, а 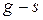 ненулевых элементов, то
ненулевых элементов, то 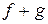 – не более чем
– не более чем 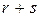 , а
, а  – не более чем
– не более чем 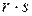 ненулевых элементов.
ненулевых элементов.
Теорема 1. Операции сложения и умножения многочленов удовлетворяют следующим свойствам:
1) ассоциативность сложения и умножения многочленов, т.е. 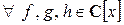 выполняются равенства
выполняются равенства 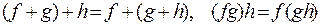 ;
;
2) коммутативность сложения и умножения многочленов, т.е. 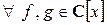 выполняются равенства
выполняются равенства  ;
;
3) дистрибутивность умножения относительно сложения, т.е. 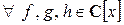 выполняется
выполняется 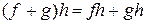 ;
;
4) для многочлена вида 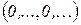 и
и 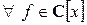 выполняется
выполняется 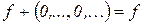 ;
;
5) для многочлена вида 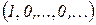 и
и 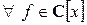 выполняется
выполняется 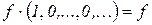 .
.
Доказательство. Проверим ассоциативность умножения. Пусть
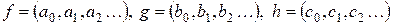 .
.
Необходимо доказать, что 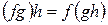 . Имеем:
. Имеем:
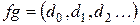 , где
, где 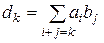 .
.
Тогда
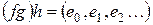 ,
,
где
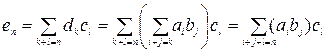 ,
,
и
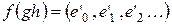 , где
, где 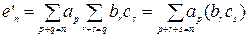 ,
,
то есть ассоциативность умножения выполняется в силу ассоциативности умножения в 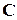 .
.
Проверим дистрибутивность, то есть выполнение равенства
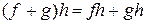 .
.
Имеем 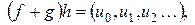 где
где 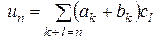 ;
;
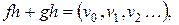 где
где 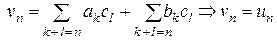 .
.
Проверим коммутативность умножения. Имеем
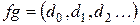 , где
, где 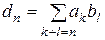 и
и
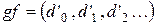 , где
, где 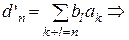
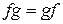 в силу коммутативности умножения в С.
в силу коммутативности умножения в С.
Аналогично проверяются остальные свойства. ■
Рассмотрим  . Очевидно, что
. Очевидно, что
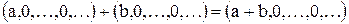
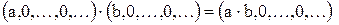 .
.
Следовательно, множество С' можно отождествить с С (то есть построить взаимно однозначное соответствие между этими множествами, так что 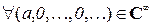 ставится в соответствие
ставится в соответствие 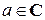 .)
.)
Обозначим 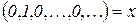 (так как
(так как 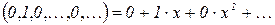 ).
).
Утверждение 1.Пусть 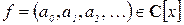 . Тогда
. Тогда 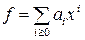 .
.
Доказательство. Так как 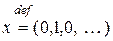 , то легко видеть, что
, то легко видеть, что 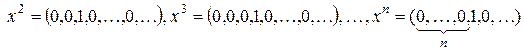 . Тогда
. Тогда
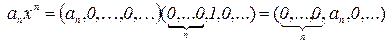 , и, значит
, и, значит
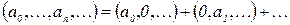
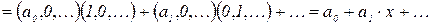 ■
■
Терминология. Пусть 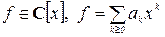 . Тогда
. Тогда 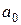 называется свободным членом многочлена. Если
называется свободным членом многочлена. Если 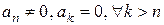 , то
, то 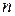 называется степенью многочлена. Пишут
называется степенью многочлена. Пишут 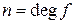 (degree),
(degree), 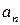 – старший коэффициент
– старший коэффициент 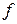 ,
, 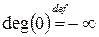 ,
, 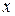 – переменная.
– переменная.
Следствие. 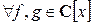 выполняется
выполняется 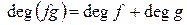 .
.
При этом 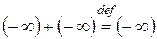 ,
, 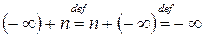 .
.
Доказательство. Пусть 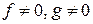 и
и 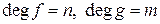 . Тогда
. Тогда 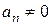 и
и 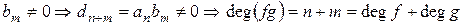 .
.
Если 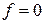 или
или 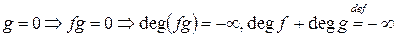 .■
.■
Замечание. 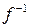 определено только для многочленов нулевой степени
определено только для многочленов нулевой степени 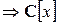 близко по свойствам к множеству целых чисел
близко по свойствам к множеству целых чисел 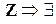 алгоритм деления с остатком.
алгоритм деления с остатком.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|