- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.. Дискретная случайная величина (ДСВ). Непрерывная случайная величина (НСВ). ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
Дискретная случайная величина (ДСВ)
все возможные её значения изолированы друг от друга.
Непрерывная случайная величина (НСВ)
все возможные её значения заполняют некоторый конечный или бесконечный интервал.
Способ задания:
Закон распределения - соответствие между возможными значениями случайной величины и их вероятностями.
| X | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
Плотность распределения вероятностей – дифференциальный закон распределения непрерывной случайной величины. 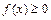
Интегрируя плотность распределения в интервале (х1,х2), вычисляем вероятность попадания НСВ в заданный интервал 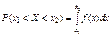 , причём
, причём 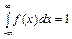
Функция распределения случайной величины равна вероятности того, что случайная величина Х примет значение меньше некоторого фиксированного х. 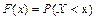 ,
, 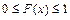
График – ступенчатая возрастающая функция
Непрерывная возрастающая функция. 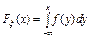
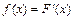 ;
; 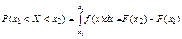
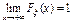 ;
; 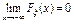
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.
1. Математическое ожидание -«среднее ожидаемое значение» случайной величины.
Для ДСВ - сумма произведений всех её значений на их вероятности
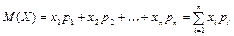
Для НСВ – интеграл от произведения её значения на функцию плотности вероятности
М(X)= 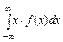
2. Дисперсия случайной величины – показатель разброса значений случайной величины вокруг её «среднего значения» Дисперсия равна математическому ожиданию квадрата отклонения случайной величины от её математического ожидания. 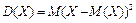
Дисперсия как разность математических ожиданий: 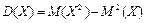
Дисперсия ДСВ:
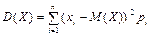 , или
, или 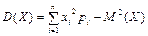
Дисперсия НСВ: 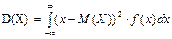
или 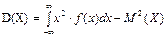
3. Среднее квадратическое отклонение - величина, равная корню из дисперсии случайной величины 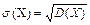
4. Мода –наиболее вероятное значение случайной величины
Значение ДСВ xkс наибольшей вероятностью pk
Значение НСВ, при котором функция плотности достигает своего наибольшего значения.
5. Медиана –«середина» возможных значений случайной величины
Для ДСВ при n=2k+1, me=xk, а при n=2k, me= 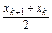
Для НСВ, meищем из уравнения:
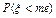 =
= 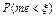
6. Начальный момент n-го порядка случайной величины 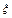 равен математическому ожиданию величины
равен математическому ожиданию величины 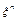 :М(
:М( 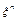 )=
)= 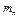
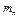 =
= 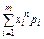
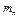 =
= 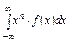
7. Центральный момент n-го порядка случайной величины 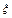 равен математическому ожиданиюn-ой степени отклонения СВ от её мат.ожидания
равен математическому ожиданиюn-ой степени отклонения СВ от её мат.ожидания
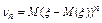
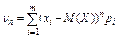
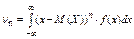
Примеры непрерывных распределений:
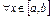 ,
, 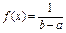
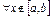 ;
; 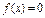 Функция распределения
Функция распределения
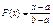 ,
Числовые характеристики:
,
Числовые характеристики:
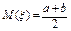 ,
, 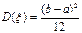
2) нормальное (Гауссовское) распределение с параметрами аи 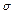 :
:
Функция плотности нормального распределения :
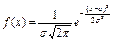 ,
,
М( 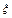 )=
)= 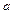 , а
, а 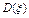 =
= 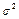
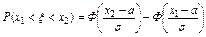 , где Ф(х)- функция Лапласа.
, где Ф(х)- функция Лапласа.
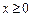 ,
, 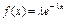 ,
при
,
при 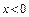 ,
, 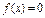 ,
Функция распределения
,
Функция распределения 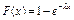 ,
Числовые характеристики:
,
Числовые характеристики: