СЛУЧАЙНЫЕ СОБЫТИЯ.

СЛУЧАЙНЫЕ СОБЫТИЯ.

1.Под случайным явлением понимается явление с неопределённым исходом, которое при неоднократном воспроизведении некоторого комплекса условий происходит по разному.

2.Под испытанием в т/в понимают реализацию определённого комплекса условий, который может быть воспроизведён сколько угодно раз. Задать испытание в т/в, значит задать множество его элементарных исходов -W.

3. Случайным называется такое событие, которое может наступить или не наступить в результате испытания.

4. Для любого события “А”, множество элементарных исходов разделяется на два подмножества: подмножество благоприятных исходов(т.е. исходов, вместе с каждым из которых наступает событие “А”) и подмножество неблагоприятных исходов. (при реализации которых событие“A” не происходит.). Если событие не может быть разбито на более мелкие, то оно называется элементарным.

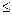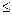5. Классическое определение вероятности: Для испытания с конечным числом равновозможных исходов вероятность случайного события “A” обозначается Р(А) и определяется как отношение числа благоприятных исходов m к общему числу n элементарных исходов испытания:Р(А) = m/n. Вероятность случайного события принимает значения от 0 до 1. 0 Р(А) 1

6.Событие, которое никогда ни происходит в результате испытания, называется невозможным.Вероятность невозможного события равна 0.

7. Событие, которое всегда происходит при испытании, называется достоверным. Вероятность достоверного события равна 1.

8.Два события называются несовместными, если появление одного в результате испытания исключает появление другого.

9. Произведением или пересечением двух событий “А” и “В” называется новое событие С = А۰В = А ∩ В, заключающееся в одновременном наступлении событий “А” и “В”.

10. Условная вероятность -Р_В(А) -вероятность появления события А, при условии, что событие В уже произошло.

Она равна отношению вероятности совместного наступления событий А и В к вероятности события В.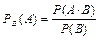

11.События А и В независимы, если Р(А)=Р_В(А) и Р(В)=Р_А(В).

12. Вероятность произведения двух зависимых событий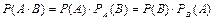

13.Вероятность произведения двух независимых событий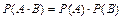

14. Суммой или объединением двух событий А + В = A 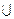B, называется новое событие, которое состоит в том, что произошло хотя бы одно из событий, т.е. или событие “А”, или “В”, или “А” и “В”. Если события “А” и “В” - несовместные, то сумма “А + В” заключается в появлении одного из них.

15.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. Р(А+В) = Р(А) + Р(В) - Р(АВ) – вероятность суммы совместных событий.

18. Вероятность суммы несовместных событий равна сумме вероятностей этих событий - Р(А+В)=Р(А)+Р(В)

16. Противоположным событием для события “A” называется новое событие, состоящее в том, что событие “A” не произошло.

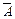- происходит тогда и только тогда, когда событие 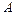не происходит. Вероятность противоположного события: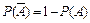

17. Пусть дано nсобытий :“А₁, А₂, … А_n”. Эти события образуют полную группу, если в результате испытания обязательно появится хотя бы одно из них. События, образующие полную группу, попарно несовместны и их сумма – достоверное событие. Сумма вероятностей событий, образующих полную группу, равна единице.

19. Формула полной вероятности.

Пусть появление некоторого события А возможно лишь при наступлении одного n из попарно несовместных событий В_i, образующих полную группу и называемых гипотезами. Тогда вероятность события А равна сумме попарных произведений вероятности каждого из этих гипотез В_i на соответствующую условную вероятность появления события А.

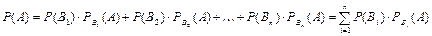
20. Формулы Байеса.

Пусть появление в некотором испытании события А возможно лишь при наступлении одного n из попарно несовместных событий В_i, образующих полную группу и называемых гипотезами. Тогда, зная вероятности гипотез Р(В_i) до проведения испытания, мы можем переоценить их после проведения испытания, в результате которого появилось событие А.

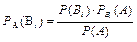, где Р(В_i) – вероятности гипотез, известные до испытания, Р(А) – полная вероятность события А,

Р_А(В_i) - вероятности гипотез, вычисленные после проведения испытания, при условии, что событие А произошло.

21. Схема Бернулли - последовательность независимых испытаний (т.е. таких испытаний, вероятность исходов которых не зависит ни от номера испытания, ни от результатов предшествующих испытаний) с двумя возможными исходами. Вероятность первого исхода - А, называемого успехом, в каждом испытаний равна «р» (Р(А)=р), тогда вероятность второго исхода – неуспеха - Р( 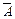)=1-р=q.

23. Формула Бернулли позволяет определить, какова вероятность того, что в серии изn испытаний по схеме Бернулли, событие А произойдёт ровно k раз: 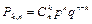, где р – вероятность наступления события А в одном испытании, q –вероятность не наступления события А в одном испытании, n – общее число испытаний, k – число успехов в серии из n испытаний, 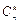число сочетаний из “n” элементов по “k” элементов в каждом.

24. Сочетаниями из “n” элементов по “k” элементов в каждом, называются “k” элементные подмножества “n” элементного множества. Два сочетания отличаются друг от друга только составом элементов, но не их порядком.

Число сочетаний из “n” элементов по “k” элементов в каждом равно 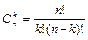, где .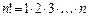

25. Закон Пуассона распределения вероятностей массовых и редких событий. 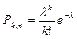, где 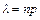, n – общее число независимых испытаний, р – вероятность «успеха» в одном испытании, - вероятность того, что в серии из n испытаний «успех» произойдёт ровно k раз. Формула Пуассона применяется, когда n – очень велико, а р – достаточно мало.

12 Следующая ⇒