
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА 2 страница
Частный случай общей поставки задачи.
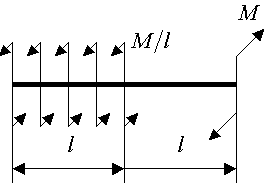
Пусть все действующие силы лежат в одной плоскости – например, листа. Выберем за центр приведения точку О – в этой же плоскости. Получим результирующую силу 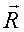 и результирующую пару и результирующую пару 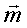 в этой же плоскости, то есть в этой же плоскости, то есть 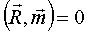 (рис.19) (рис.19)
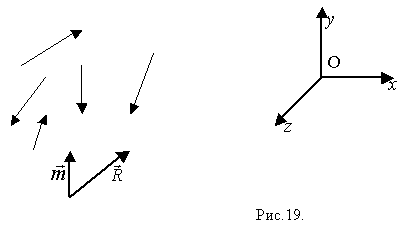 Замечание.
Систему можно привести к одной результирующей силе.
Условия равновесия:
Замечание.
Систему можно привести к одной результирующей силе.
Условия равновесия:
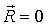 , , 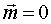 или скалярные:
или скалярные:
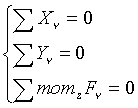 Очень часто встречаются в приложениях, например, в сопротивлении материалов.
Пример.
Очень часто встречаются в приложениях, например, в сопротивлении материалов.
Пример.
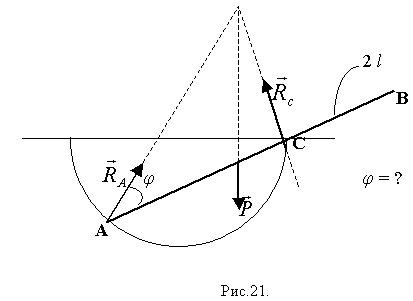
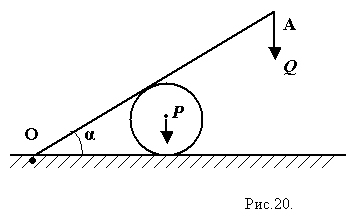 С трением шара о доску и о плоскость. Условие равновесия:
С трением шара о доску и о плоскость. Условие равновесия:  = ?
Задача о равновесии несвободного твёрдого тела.
Несвободным называется такое твёрдое тело, перемещение которого стеснено связями. Например, другими телами, шарнирными закреплениями.
При определении условий равновесия: несвободное тело можно рассматривать как свободное, заменяя связи неизвестными силами реакции.
Пример. = ?
Задача о равновесии несвободного твёрдого тела.
Несвободным называется такое твёрдое тело, перемещение которого стеснено связями. Например, другими телами, шарнирными закреплениями.
При определении условий равновесия: несвободное тело можно рассматривать как свободное, заменяя связи неизвестными силами реакции.
Пример.
 Контрольные вопросы:
1. Что называется плоской системой сил?
2. Напишите условия равновесия плоской системы сил.
3. Какое твёрдое тело называется несвободным?
Контрольные вопросы:
1. Что называется плоской системой сил?
2. Напишите условия равновесия плоской системы сил.
3. Какое твёрдое тело называется несвободным?
|
| Лекция 5.Частные случаи равновесия твёрдого тела. |
| Теорема. Три силы уравновешивают твёрдое тело только в том случае, когда все они лежат в одной плоскости.
Доказательство. Выберем за точку приведения точку на линии действия третьей силы. Тогда
Рис.22.
То есть плоскости
Условия равновесия твёрдого тела с одной неподвижной точкой. Центр приведения – закреплённая точка (рис.23):
Рис.23.
Моменты (условия равновесия):
Для определения реакций => результирующая:
Условия равновесия твёрдого тела, способного вращаться вокруг неподвижной оси.
Рис.24.
Закреплены две точки О и О1. Центр приведения: точка О (рис.24).
Уравнения равновесия:
Положение тела в пространстве определяется одним параметром, например, углом поворота
Условия равновесия твёрдого тела, способного перемещаться параллельно неподвижной плоскости (рис.25).
Рис.25.
Уравнения равновесия:
где Два первых и последнее уравнения – необходимые условия равновесия. Три остальных => реакции, то есть только для закрепления в трёх точках. Иначе => статически неопределимая задача.
Случай опоры на три точки. Для определения реакций имеем:
где
Решение имеется только при условии:
то есть три точки опоры не лежат на одной прямой. Иначе, статическая неопределимость.
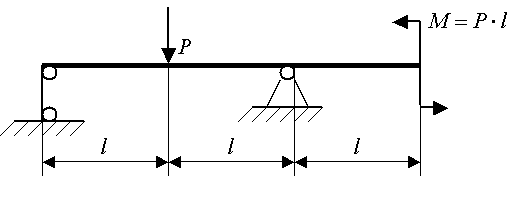
Пример.
Рис.26.
Если дано, что опора упругая =>
Тогда для реакции: (удобно взять начало координат в одной из опор).
Контрольные вопросы: 1. В каком случае три силы уравновешивают твёрдое тело? 2. Как выглядят условия равновесия тела с одной неподвижной точкой? 3. Напишите уравнения равновесия тела, способного вращаться вокруг неподвижной оси. | ||||||
| Лекция 6.Задача о равновесии бруса. |
| Виды опор:
Рис.27. Уравнения равновесия:
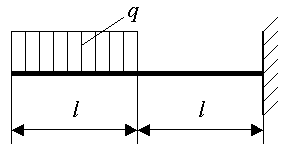
Виды нагрузок:
Рис.28. Найти: RA, RB.
Проверка:
Контрольные вопросы: 1. Назовите виды опор в ???????? схемах. 2. Чем отличаются шарнирно подвижная и шарнирно неподвижная опоры? 3. Какие уравнения являются наиболее удобными для нахождения реакций в брусе | |||
| Лекция 7.Определение внутренних усилий в стержневых конструкциях. |
Внутренние усилия определяются методом сечений (РОЗУ), состоящим из четырёх этапов:
Р – рассекаем, то есть проводим сечение в том месте, где определяются внутренние усилия;
О – отбрасываем одну из частей и рассматриваем оставшуюся часть;
З – заменяем действие отброшенной части на рассматриваемую внутренними усилиями, которые приводим к центру тяжести сечения. Проецируя приведённые усилия на оси, получаем следующие неизвестные:
N – продольная сила;
Qy, Qz – поперечные силы;
Мкр – крутящий момент;
My, Mz – изгибающие моменты.
Эти усилия направляются в соответствии с правилами статики для выбранной системы координат:
Рис.29. У – уравновешиваем, то есть составляем шесть уравнений равновесия, из которых и определяются внутренние усилия. Затем строятся графики внутренних усилий вдоль оси бруса, которые называются эпюрами внутренних усилий.
Частные случаи. 1) Изгиб ( Qz, My ).
2) Изгиб ( Qz, My ).
3)Растяжение, сжатие ( N ).
4) Кручение ( Мкр ).
Рис.30. Контрольные вопросы: 1. Из каких этапов состоит метод сечений? 2. Что называется эпюрой внутреннего усилия? 3. Перечислите основные частные случаи нагружения бруса. | ||
| Лекция 8.Основы кинематики точки. |
Кинематикой называется та часть механики, в которой изучаются зависимости между величинами, характеризующими состояние систем, но не рассматриваются причины вызывающие изменение состояние движения.
Кинематика точки. Декартовы координаты.
С неподвижной системой отсчёта связываем декартовую ортогональную систему координат (правую, рис. 31).
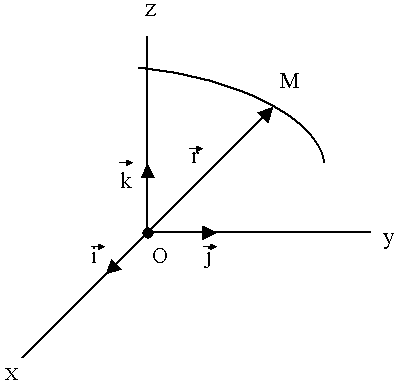 Рис.31.
Точка
Рис.31.
Точка 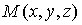 , где , где
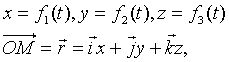 – параметрические уравнения траектории.
где – параметрические уравнения траектории.
где 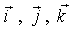 - единичные векторы (орты), - единичные векторы (орты),
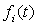 - непрерывны и 2 раза дифференцируемы; 2-е производные – непрерывны.
Непрерывная последовательность точек среды (пространства), занимаемая точкой M, называется траекторией точки М.
Исключая время: - непрерывны и 2 раза дифференцируемы; 2-е производные – непрерывны.
Непрерывная последовательность точек среды (пространства), занимаемая точкой M, называется траекторией точки М.
Исключая время:
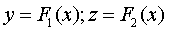 или:
или:
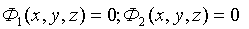 Введём понятия скорости и ускорения:
Введём понятия скорости и ускорения:
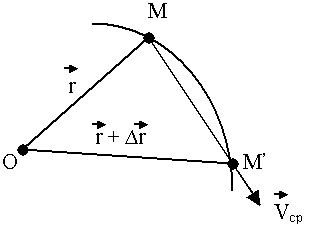
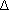 Рис.32.
т. М Рис.32.
т. М  t
т. М’ t
т. М’  t + t + 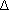 t
( t
( 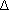 t - конечное).
Радиусы – векторы: t t - конечное).
Радиусы – векторы: t  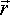 t +
t + 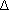 t t  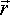 + + 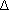 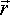
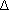 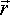 = = 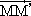 За время
За время 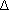 t (рис. 32): t (рис. 32):
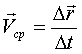 (Направление по секущей MM’).
Скорость точки в момент времени t получается при (Направление по секущей MM’).
Скорость точки в момент времени t получается при 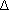 t t  0, то есть 0, то есть
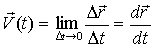 (Направление по касательной и траектории точки)
Очевидно: (Направление по касательной и траектории точки)
Очевидно:
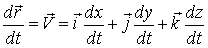 Проекции
Проекции 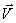 : :
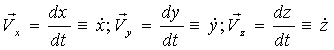 .
Модуль (длина): .
Модуль (длина):
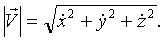 Скорость точки М в момент времени t равна производной по времени от радиуса – вектора точки и направлена по касательной к траектории.
Аналогично найдём ускорение (рис. 33).
Скорость точки М в момент времени t равна производной по времени от радиуса – вектора точки и направлена по касательной к траектории.
Аналогично найдём ускорение (рис. 33).
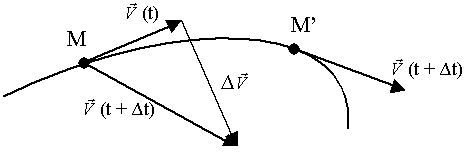 Рис.33.
Совмещая начало векторов
Рис.33.
Совмещая начало векторов 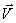 (t) и (t) и 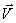 (t + (t + 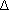 t) в точке М => t) в точке М => 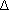 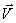 за за 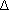 t.
Среднее ускорение: t.
Среднее ускорение:
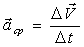 (направление в сторону вогнутости траектории)
Ускорение точки в момент времени t получается при (направление в сторону вогнутости траектории)
Ускорение точки в момент времени t получается при 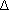 t t  0, то есть 0, то есть
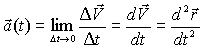 Очевидно:
Очевидно:
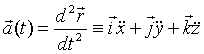
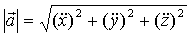 Ускорение точки в некоторый момент времени равно производной по времени от вектора скорости, или второй производной по времени от радиуса – вектора точки в этот момент времени.
В некоторых задачах – используется производная более высоких порядков, но здесь они пока не нужны.
В механике применяются не только декартовы координаты – часто применяют обобщённые (криволинейные) координаты.
Они бывают удобней, позволяют определить конфигурацию рассматриваемой системы. Часто их называют позиционными. Криволинейными они называются потому, что линии вдоль которых меняется только одна координата, обычно бывают кривыми.
Рассмотрим частный случай криволинейных координат – полярные координаты точки на плоскости: применим далее к задаче движение точек в центральном силовом поле (рис. 34).
Ускорение точки в некоторый момент времени равно производной по времени от вектора скорости, или второй производной по времени от радиуса – вектора точки в этот момент времени.
В некоторых задачах – используется производная более высоких порядков, но здесь они пока не нужны.
В механике применяются не только декартовы координаты – часто применяют обобщённые (криволинейные) координаты.
Они бывают удобней, позволяют определить конфигурацию рассматриваемой системы. Часто их называют позиционными. Криволинейными они называются потому, что линии вдоль которых меняется только одна координата, обычно бывают кривыми.
Рассмотрим частный случай криволинейных координат – полярные координаты точки на плоскости: применим далее к задаче движение точек в центральном силовом поле (рис. 34).
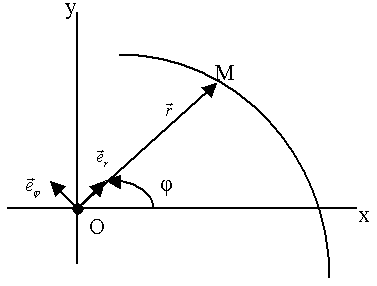 Рис.34.
(x, y) – декартовы координаты.
(r,
Рис.34.
(x, y) – декартовы координаты.
(r, 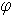 ) – полярные координаты.
Угол ) – полярные координаты.
Угол 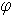 => от Ох против часовой стрелки – положительное направление
Формулы преобразования:
x = r cos => от Ох против часовой стрелки – положительное направление
Формулы преобразования:
x = r cos 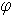 , y = r sin , y = r sin 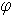 , где r , где r 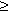 0; 0 0; 0 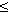 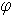 < 2 < 2  (можно рассматривать и
(можно рассматривать и 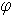  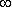 ).
Если r = const – концентрические окружности с центром в точке О.
Если ).
Если r = const – концентрические окружности с центром в точке О.
Если 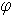 = const – прямолинейные лучи из точки О.
Введём два орта: = const – прямолинейные лучи из точки О.
Введём два орта:
 Найдём производные
Найдём производные 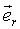 по углу по углу 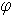 (рис. 35): (рис. 35):
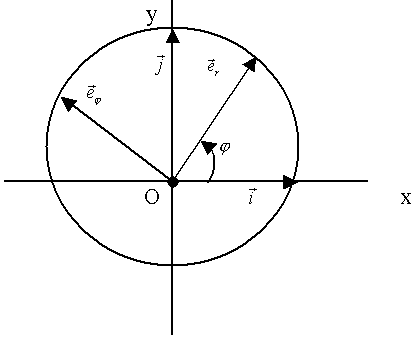 Рис.35.
Рис.35.
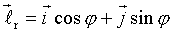 (так как r = 1) (так как r = 1)
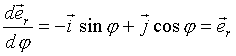 при при 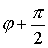 ,
т. е. ,
т. е. 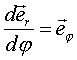 .
Далее: .
Далее:
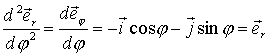 при при 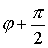 ,
т. е. ,
т. е. 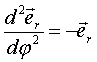 .
При каждом дифференцировании по φ т. е. происходит поворот на угол .
При каждом дифференцировании по φ т. е. происходит поворот на угол 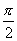 .
Выведем формулы проекции скорости и ускорения точки М на направления касательных к координатным линиям в полярных координатах.
Так как .
Выведем формулы проекции скорости и ускорения точки М на направления касательных к координатным линиям в полярных координатах.
Так как 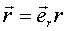 , то , то
 Но:
Но: 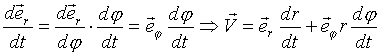 Очевидно:
Очевидно:
 Для ускорения:
Для ускорения:
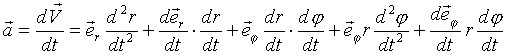 .
Но: .
Но: 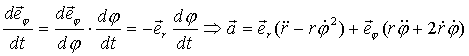 .
Очевидно: .
Очевидно:
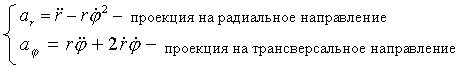 Контрольные вопросы:
1. Что изучает кинематика?
2. Дайте определение скорости точки.
3. Напишите формулы проекций ускорения на оси полярной системы координат.
Контрольные вопросы:
1. Что изучает кинематика?
2. Дайте определение скорости точки.
3. Напишите формулы проекций ускорения на оси полярной системы координат.
|
| Лекция 9.Естественные координаты. |
Рассмотрим систему координатных осей, определяемую траекторией точки (рис.36).
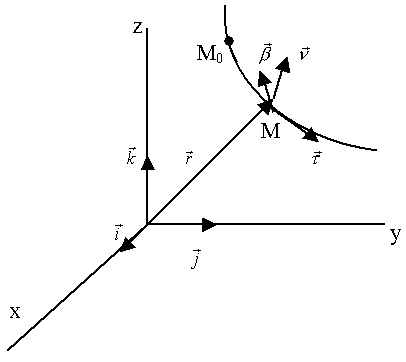 Рис.36.
Рис.36.
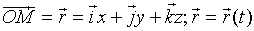 .
Единичный вектор касательной к траектории (S – длина дуги М0М): .
Единичный вектор касательной к траектории (S – длина дуги М0М):
 , где , где 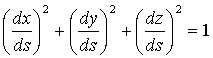 .
Дифференцируя .
Дифференцируя 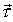 по S: по S: 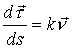 ,
где ,
где 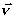 - единичный вектор главной нормали; - единичный вектор главной нормали; 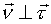 и направлен в сторону вогнутости; и направлен в сторону вогнутости;
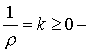 кривизна. (k = 0 - прямая); кривизна. (k = 0 - прямая); 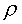 - радиус кривизны.
Единичный вектор бинормали - радиус кривизны.
Единичный вектор бинормали 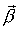 : :
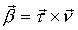 . .
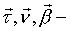 образуют правую тройку ортогональных единичных векторов. Они определяют направление естественных (натуральных) осей в том месте траектории, где находится движущаяся точка. образуют правую тройку ортогональных единичных векторов. Они определяют направление естественных (натуральных) осей в том месте траектории, где находится движущаяся точка.
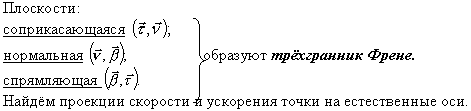 соприкасающаяся соприкасающаяся 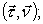
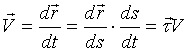 Очевидно, проекция на ось
Очевидно, проекция на ось 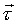 : : 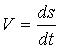 (может иметь разные знаки – зависит от направления S).
Для ускорения: (может иметь разные знаки – зависит от направления S).
Для ускорения:
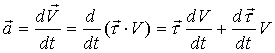 ;
Но: ;
Но: 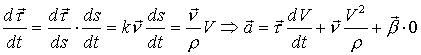 ;
Очевидно, проекции ускорения на естественные оси:
на касательную: ;
Очевидно, проекции ускорения на естественные оси:
на касательную: 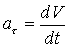 ;
на главную нормаль: ;
на главную нормаль: 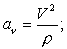 на бинормаль: 0
Таким образом, ускорение лежит в соприкасающейся плоскости (рис. 37).
на бинормаль: 0
Таким образом, ускорение лежит в соприкасающейся плоскости (рис. 37).
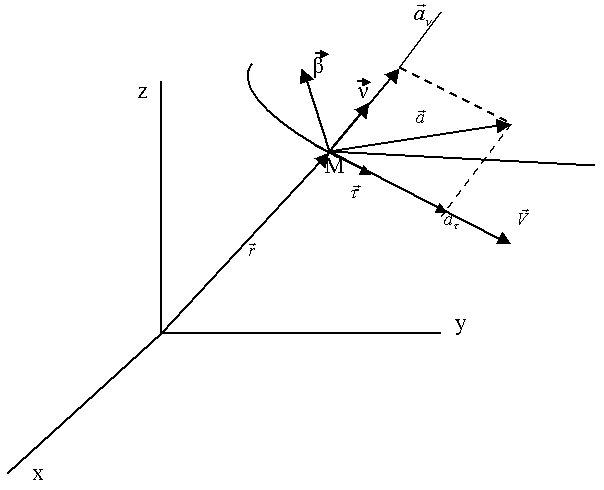 Рис.37.
Задача.
Рис.37.
Задача.
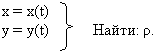
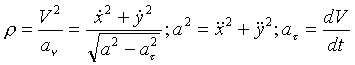 Контрольные вопросы:
1. Какие основные отличия естественной системы координат от декартовой?
2. Назовите проекции скорости точки в естественных координатах.
3. Какова последовательность определения радиуса кривизны траектории точки?
Контрольные вопросы:
1. Какие основные отличия естественной системы координат от декартовой?
2. Назовите проекции скорости точки в естественных координатах.
3. Какова последовательность определения радиуса кривизны траектории точки?
|
| Лекция 10.Формула Эйлера. |
Найдём число координат, определяющих положение абсолютно твёрдого тела.
Определить положение тела => определить координаты  точки относительно некоторой системы отсчёта в точки относительно некоторой системы отсчёта в  момент времени. момент времени.
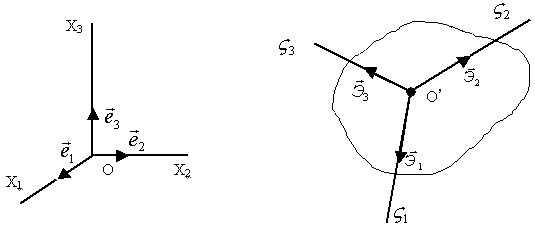 Рис.38.
Пусть Х1 , Х2 , Х3 – неподвижные оси (рис. 38); орты:
Рис.38.
Пусть Х1 , Х2 , Х3 – неподвижные оси (рис. 38); орты: 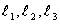 [декартова система]. [декартова система].
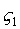 , , 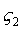 , ,  - оси, жёстко связанные с телом; орты: - оси, жёстко связанные с телом; орты: 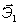 , , 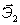 , , 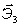 - [декартова система].
Так как координаты точек относительно собственных осей - [декартова система].
Так как координаты точек относительно собственных осей 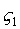 , , 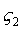 , ,  не зависят от времени, то задача сводится к определению положения координатных осей, жёстко связанных с телом (подвижных), относительно неподвижных осей Х1 , Х2 , Х3.
Составим таблицу косинусов углов между осями Х и не зависят от времени, то задача сводится к определению положения координатных осей, жёстко связанных с телом (подвижных), относительно неподвижных осей Х1 , Х2 , Х3.
Составим таблицу косинусов углов между осями Х и 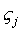 : :
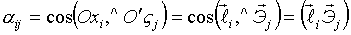
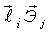 - скалярное произведение. - скалярное произведение.
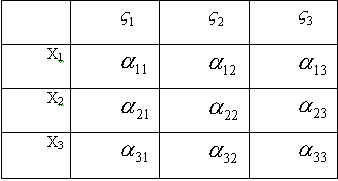 Так как системы координат ортогональны, то
скалярное произведение:
Так как системы координат ортогональны, то
скалярное произведение: 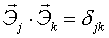 , где , где 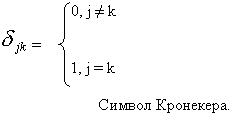
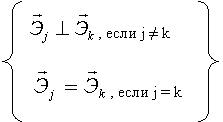
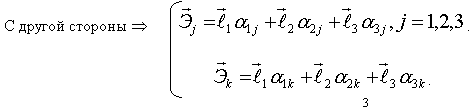
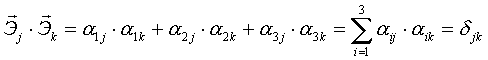 Итак:
Итак: 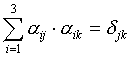 Число таких соотношений = 6 (Из 9 – ти в силу симметрии по jи k).
Число таких соотношений = 6 (Из 9 – ти в силу симметрии по jи k).
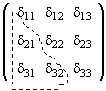 Имеем 6 соотношений для 9 косинусов =>
3 косинуса Имеем 6 соотношений для 9 косинусов =>
3 косинуса 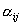 , не расположенные в одном столбце, или в одной строке, могут быть приняты за независимые, а остальные можем определить из составленных 6 – ти соотношений.
Кроме того => три координаты определяют положение точки О’ – начало системы , не расположенные в одном столбце, или в одной строке, могут быть приняты за независимые, а остальные можем определить из составленных 6 – ти соотношений.
Кроме того => три координаты определяют положение точки О’ – начало системы 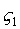 , , 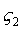 , ,  .
Но 9 координат и 3 соотношение длин: .
Но 9 координат и 3 соотношение длин:
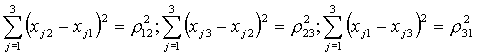 Это условия постоянства расстояний между точками в абсолютно твёрдом теле.
Выведем формулу Эйлера для распределения скоростей точек абсолютно твёрдого тела (рис. 39).
Это условия постоянства расстояний между точками в абсолютно твёрдом теле.
Выведем формулу Эйлера для распределения скоростей точек абсолютно твёрдого тела (рис. 39).
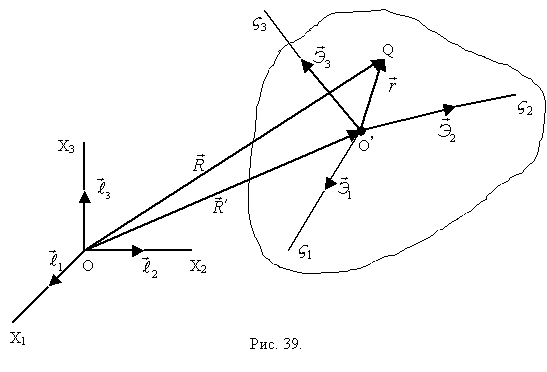
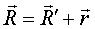 ,
1) ,
1) 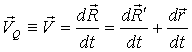 , ,
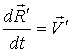 - скорость точки О’, - скорость точки О’,
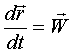 - скорость точки Q во вращательном движении тела (так как длина - скорость точки Q во вращательном движении тела (так как длина 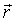 постоянна).
Так как координаты постоянна).
Так как координаты 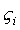 точки Qпостоянны, то точки Qпостоянны, то
 Тогда:
2)
Тогда:
2) 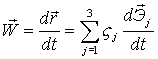 ,
где ,
где 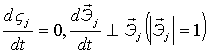 .
Скорость точки Q: .
Скорость точки Q: 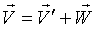 .
3) Выразим .
3) Выразим 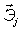 и производные через направляющие косинусы и производные через направляющие косинусы 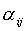 : :
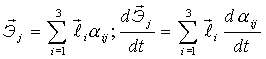 .
Тогда: .
Тогда: 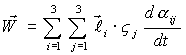 (в неподвижной системе).
4) Проекция (в неподвижной системе).
4) Проекция 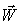 на ось на ось 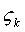 (k= 1,2,3): (k= 1,2,3):
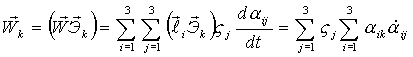 .
Скорости точек во вращательном движении – линейные функции координат точек.
5) Получим более простую и наглядную форму закона распределения скоростей, используя свойства функции .
Скорости точек во вращательном движении – линейные функции координат точек.
5) Получим более простую и наглядную форму закона распределения скоростей, используя свойства функции 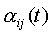 . .
 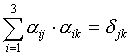 ,
Дифференцируем по t: ,
Дифференцируем по t:
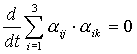 .
По свойству производной от произведения:
при j= k => .
По свойству производной от произведения:
при j= k => 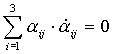 ,
при j≠ k=> ,
при j≠ k=> 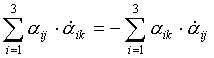 .
Свойства:
а) симметрия по kи j;
б) при j= k=>равенство «0»;
в) размерность t-1 , т. е. угловая скорость (угол в радианах), так как .
Свойства:
а) симметрия по kи j;
б) при j= k=>равенство «0»;
в) размерность t-1 , т. е. угловая скорость (угол в радианах), так как 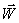 - скорость.
г) различных только три => - скорость.
г) различных только три => 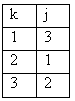 Покажем, что
Покажем, что
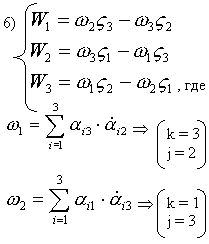
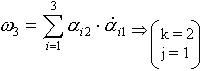 Действительно:
Действительно:
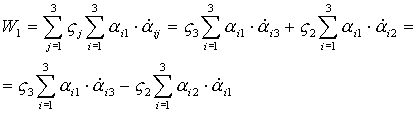
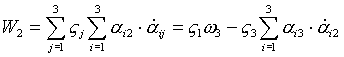
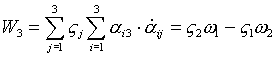 - по аналогии.
Итак: - по аналогии.
Итак:
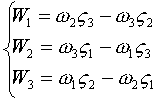 или:
7)
или:
7) 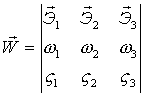 , где , где 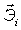 - единичные вектора, жёстко связанные с телом.
Положим - единичные вектора, жёстко связанные с телом.
Положим 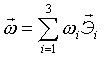 - вектор, где - вектор, где 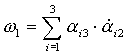
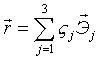 
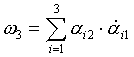 8) Тогда:
8) Тогда:
Назовём Таким образом, закон распределения скоростей точек абсолютно твёрдого тела в любом движении:
Это формула Эйлера в векторной записи.
Контрольные вопросы: 1. Сколько координат определяют положение твёрдого тела в пространстве? 2. Что называется вектором мгновенной угловой скорости? 3. Напишите формулу Эйлера. | |||
| Лекция 11.Распределение ускорений точек твёрдого тела. |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
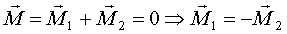 (рис.22)
(рис.22)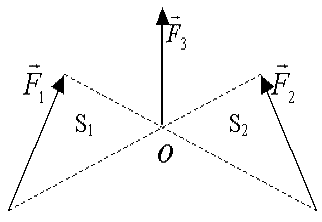
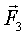 , ч.т.д. (Проще:
, ч.т.д. (Проще: 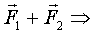 в плоскости
в плоскости 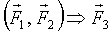 только там же для уравновешивания).
только там же для уравновешивания).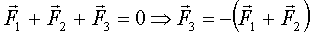
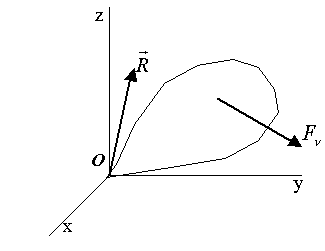
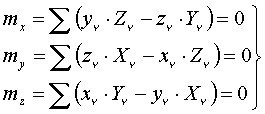
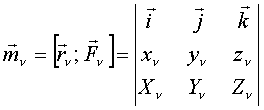
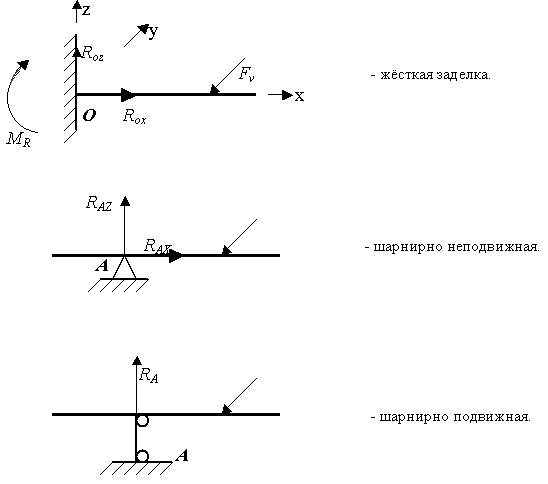
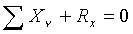 ;
; 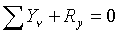 ;
; 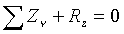 .
.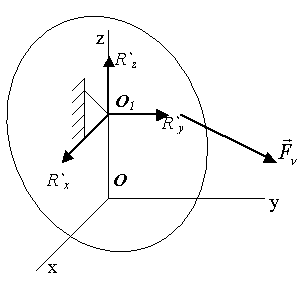
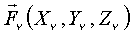 ; Rx, Ry, Rz в точке О; R`x, R`y, R`z в точке О1; ОО1 = h.
; Rx, Ry, Rz в точке О; R`x, R`y, R`z в точке О1; ОО1 = h.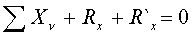
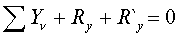
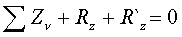
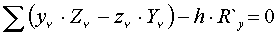
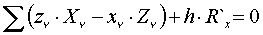
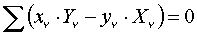
 , который определяется из последнего уравнения:
, который определяется из последнего уравнения: 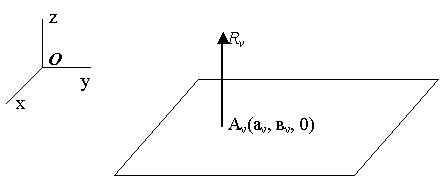
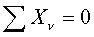
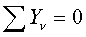

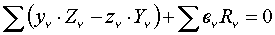
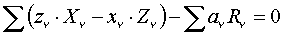
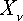 ,
, 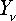 ,
, 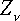 – проекции активных сил, приложенных в точках (
– проекции активных сил, приложенных в точках ( 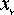 ,
, 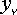 ,
, 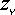 ).
).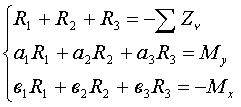 ,
,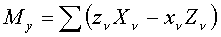 ,
,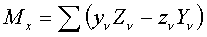 .
.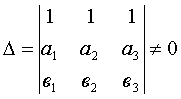 ,
,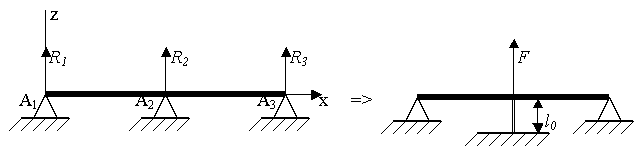
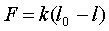 .
.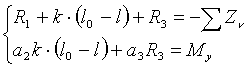
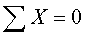

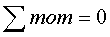
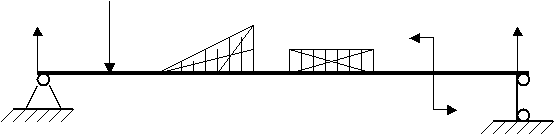
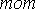 А = 0
А = 0 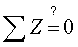
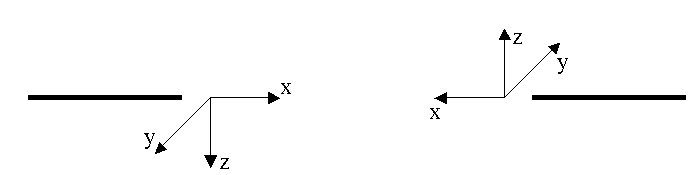
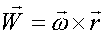
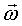 вектором мгновенной угловой скорости, а прямая на которой он располагается, в рассматриваемый момент времени, проходящую через точку О’ – осью мгновенного вращения, или мгновенной осью.
вектором мгновенной угловой скорости, а прямая на которой он располагается, в рассматриваемый момент времени, проходящую через точку О’ – осью мгновенного вращения, или мгновенной осью.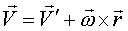 .
.