ordm; Стабильное население

17º Стабильное население

Нас будет интересовать возрастная структура населения некоторой страны, причём как мужского, так и женского. Под возрастной структурой населения в некотором году 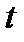понимается его распределение по возрасту в начале года. Задается она вектором 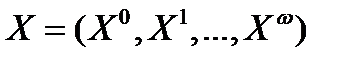, где 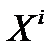- численность человек до i лет. Омега – предельный возраст.

В дальнейшем будет называть число человек, которым i лет.

Число 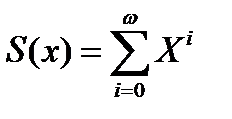совпадает с общей численностью населения, а 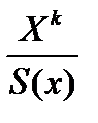указывает на число населения в возрасте 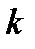лет.

Возрастную структуру женского населения обозначим через 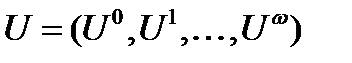, а мужского – .

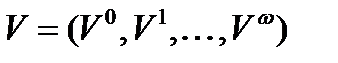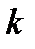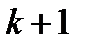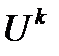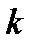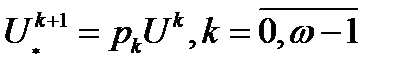Опишем движение населения во времени. Сначала остановимся на женском населении. Женщины в возрасте лет в течение года стареют на год и переходят в возрастную группу , при этом некоторая часть их умирает. Так что если численность женщин в возрасте лет в году , то (1)

Число , заключенное между нулем и единицей, называют коэффициентом дожития. Оно совпадает с вероятностью того, что женщина из группы доживет до начала следующего года. Предполагается, что женщины возраста 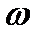, если такие имеются, не доживут до следующего года. Заметим, что равенство (1) показывает, что мы пренебрегли миграцией населения.

Введем еще коэффициенты рождаемости 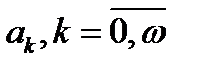, совпадающее с вероятностью того, что женщина в возрасте 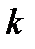лет родит в течение года девочку, дожившую до начала следующего года. Понятно, что 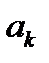равно нулю для достаточно малых и достаточно больших 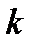. Общая численность девочек, родившихся в данном году и доживших до начала след года равна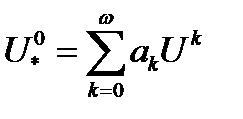

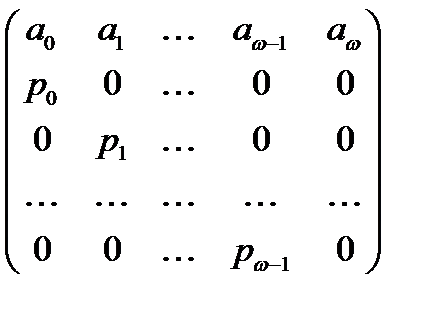Таким образом, возрастная структура женского населения U перейдет в следующем году в в структуру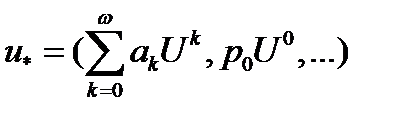

Рассмотрим матрицу размерами 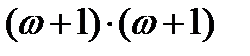, которую обычно называют матрицей Лесли.

Легко убедиться в том, что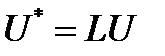

Чтобы описать движение мужского населения, надо ввести по аналогии коэффициенты дожития для мужчин 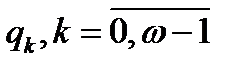. Заметим, что обычно 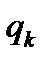отличается от 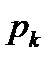, причем 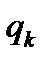меньше 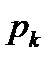, то есть мужская смертность выше.

Рождаемость мальчиков определяется в демографии так же, как и рождаемость девочек (по возрасту матери)

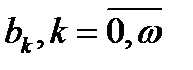как вероятность того, что женщина в возрасте 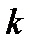лет родит в течение года мальчика, дожившего до конца года.

Обычно 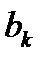немного больше, чем 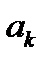. Тогда в течение года возрастная структура 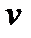мужского населения перейдет в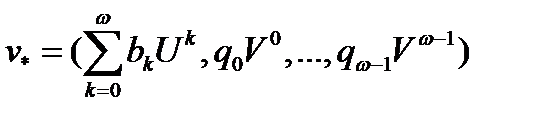

Таким образом, движение женского населения можно изучать независимо от мужского, в то время как движение мужского населения по сути дела определяется женским, поэтому в дальнейшем мы ограничимся лишь изучением движения женского населения. Конечно, более точное описание ситуации требует совместного рассмотрения и мужского, и женского населения. Для этого надо ввести оператор заключения брака. Это существенно усложняет модель, хотя качественный характер выводов изменяется незначительно.

Набор коэффициентов рождаемости и дожития называют режимом воспроизводства населения. Этот режим может быть записан в виде матрицы Лесли (2). Обычно он меняется во времени крайне медленно, если не считать эпохи войн, революций и других потрясений. Поэтому в течение длительного промежутка времени его можно считать постоянным. Основную роль при исследовании движения населения с данным режимом играют собственное число и собственный вектор матрицы Лесли. Напомним, что число 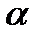называется собственным числом матрицы Л, если существует такой ненулевой вектор 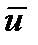, что 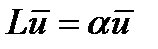. При этом 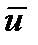называется собственным вектором. Оказывается, что матрица 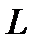имеет, и при этом только одно, положительное собственное число, которому отвечает собственный вектор 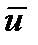с неотрицательными компонентами. Этот вектор единственен с точностью до положительного множителя.

Понятно, что общая численность женского населения 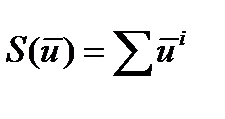изменяется при переходе от одного собственного вектора к другому. В то же время, доля населения в возрасте 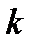лет 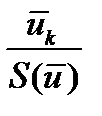не зависит от выбора собственного вектора, т.к. все они пропорциональны.

Таким образом, все собственные векторы задают одну и ту же относительную структуру населения, которая указывает доли населения соответствующего возраста. Пусть структура населения в некотором базовом году 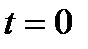задается некоторым собственным вектором, 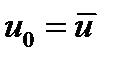. Тогда в году 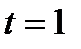будем иметь 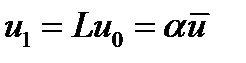. При 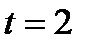получим .

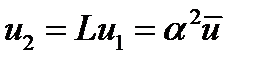Как мы видим, если исходное население задавалось собственным вектором матрицы Лесли, то движение населения во времени выразится последовательностью 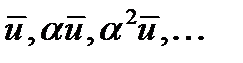. При этом относительная структура населения не меняется с течением времени, она стабильна. В связи с этим, население, описываемое собственным вектором матрицы Лесли, называется стабильным. Относительная возрастная структура такого населения не изменяется, а численность его растет как геометрическая прогрессия (по экспоненциальному закону) с показателем 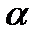, который называется темпом роста населения.

⇐ Предыдущая 11 12 13 14 151617 18 19 20 Следующая ⇒