Хелпикс

Главная

Контакты

Случайная статья



Розв'язання

Стр 1 из 3Следующая ⇒


 

Тема : Ірраціональні рівняння.

Ірраціональними називають рівняння, в яких під знаком кореня міститься змінна (невідо­ма).

Наприклад: 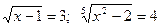— ірраціональні рів­няння.

Розв'язування ірраціональних рівнянь ґрунтується на приве­денні їх за допомогою деяких перетворень до раціонального рів­няння. Як правило, це досягається піднесенням обох частин ірра­ціонального рівняння до одного і того самого степеня (інколи декілька разів).

При піднесенні обох частин рівняння до парного степеня одер­жане рівняння може мати корені, що не задовольняють даному рівнянню. Такі корені називаються сторонніми для даного рівнян­ня. (Це відбувається тому, що із рівності парних степенів двох чисел не слідує рівність цих чисел. )

Тому слід обов'язково робити перевірку одержаних коренів.

Приклад 1.  Розв'яжіть рівняння .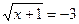

Розв'язання

Рівняння 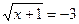 не має коренів, так як корінь с пар­ним показником не може бути від'ємним.

 

Приклад 2. Розв'язати рівняння .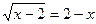

Розв'язання

 

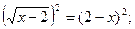
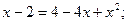
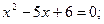
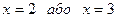
Перевірка: 1) 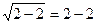;        2) .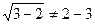

Відповідь: 2.

Приклад 3.  Розв'яжіть рівняння .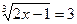

Розв'язання:

 

 

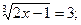
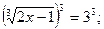
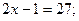
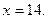
Відповідь: 14.

Приклад 4.  Розв'яжіть рівняння . 

Розв'язання:

Обидві частини рівняння піднесемо до квадрата:

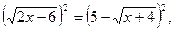одержимо

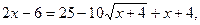
або після перетворення

 

Знову піднесемо до квадрата обидві частини рівняння:

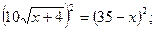
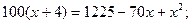
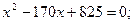
звідси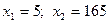

Перевірка: 1)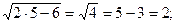  

2)  

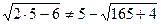
Відповідь: 5.

Приклади розв'язування ірраціональних рівняння.

1. Розв'яжіть рівняння х2 + 3х – 18 + 4 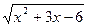 = 0 .

Розв'язання

Нехай 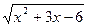= t, t > 0, тоді х2 + 3х – 18 = t2 – 12 і дане рівняння стане таким: t2 – 12 + 4t = 0, звідси t1 = – 6, t2 = 2.

1) 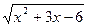 = – 6 – розв'язків немає.

2) 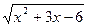 = 2, х2 + 3х – 6 = 4,  х2 + 3x – 10 = 0, звідси х = – 5 або х = 2. Перевірка показує, що – 5 і 2 — корені.

Відповідь: – 5; 2.

2. Розв'яжіть рівняння: .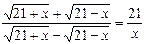


123Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.