Прямолинейная регрессия

Прямолинейная регрессия

Это наиболее простой вид регрессии, поэтому неудивительно, что если есть возможность каким-либо способом свести криволинейную регрессию к прямолинейной, то такая возможность используется. Наиболее часто при этом применяется изменение масштаба для одной или обеих переменных, например, путем замены величин на их логарифмы, квадраты, квадратные корни и пр. Подобрав способ преобразования, следует убедиться, что регрессионный анализ может быть применен к полученным преобразованным данным.

Для отыскания двух параметров 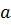и 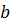в уравнении регрессии вида:

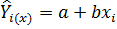
нужно иметь систему из двух уравнений. При использовании метода наименьших квадратов коэффициенты 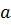и 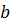находятся путем решения системы следующих уравнений:

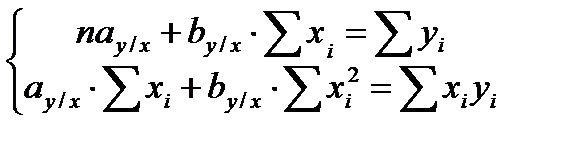
где п – число пар сопряженных точек.

Из этой системы следует, что:

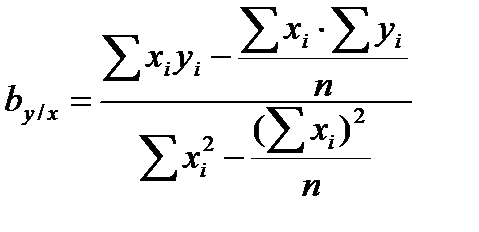
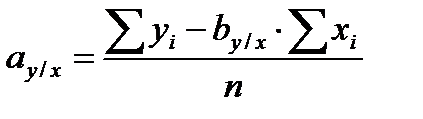Для нашего примера в итоге получаем (размерность х - %, а у - кал/г грунта):

X	y	x²	xy

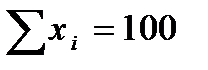
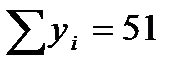
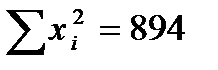
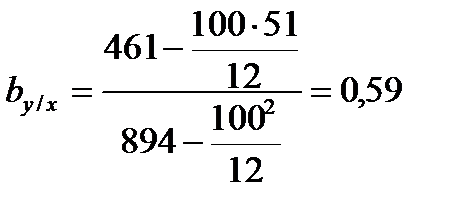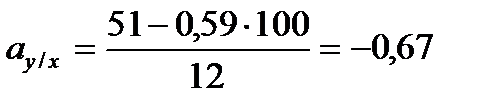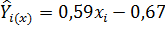
Пользуясь уравнением регрессии можно установить, чему, в среднем, равно значение зависимой переменной при заданном значении независимой переменной. Если коэффициенты в уравнении являются оценками, как это обычно и бывает, то результат вычислений будет оценкой условного среднего. Так, при х = 5,0 получим 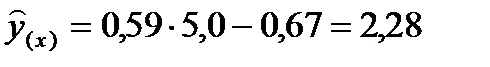кал/г.

Всякое уравнение регрессии имеет границы применимости:

§ Только для данного объекта;

§ Только в заданном интервале изменения аргумента.

Коэффициент 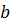характеризует прирост функционального признака при изменении признака, считаемого аргументом, на единицу и, таким образом, является размерной величиной. Ее размерность представляет собой отношение размерности функционального признака к размерности признака, взятого как аргумент. В нашем примере: .

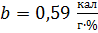Если регрессионный анализ проводится на корреляционной модели, то в качестве аргумента может быть выбран как признак х, так и признак у. Этим случаям соответствуют два разных уравнения регрессии:

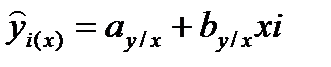– для y по x

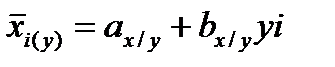– для x по y

где 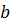_y_/_x характеризует изменение у по х, а 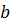_x_/_y – х по у.

Нахождение параметров а_x_/_y и в_y_/_x осуществляется с помощью уже приведенных выражений, в которых индексы х заменены на у.

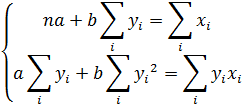
Для нашего примера:

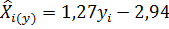
При корреляционных связях абсолютная величина любого коэффициента регрессии всегда меньше обратной величины другого:

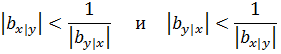
в силу чего эти коэффициенты и именуются коэффициентами регрессии (от латинского regressio - движение назад), и различия эти тем значительнее, чем сильнее изучаемая связь отличается от прямолинейной функциональной зависимости.

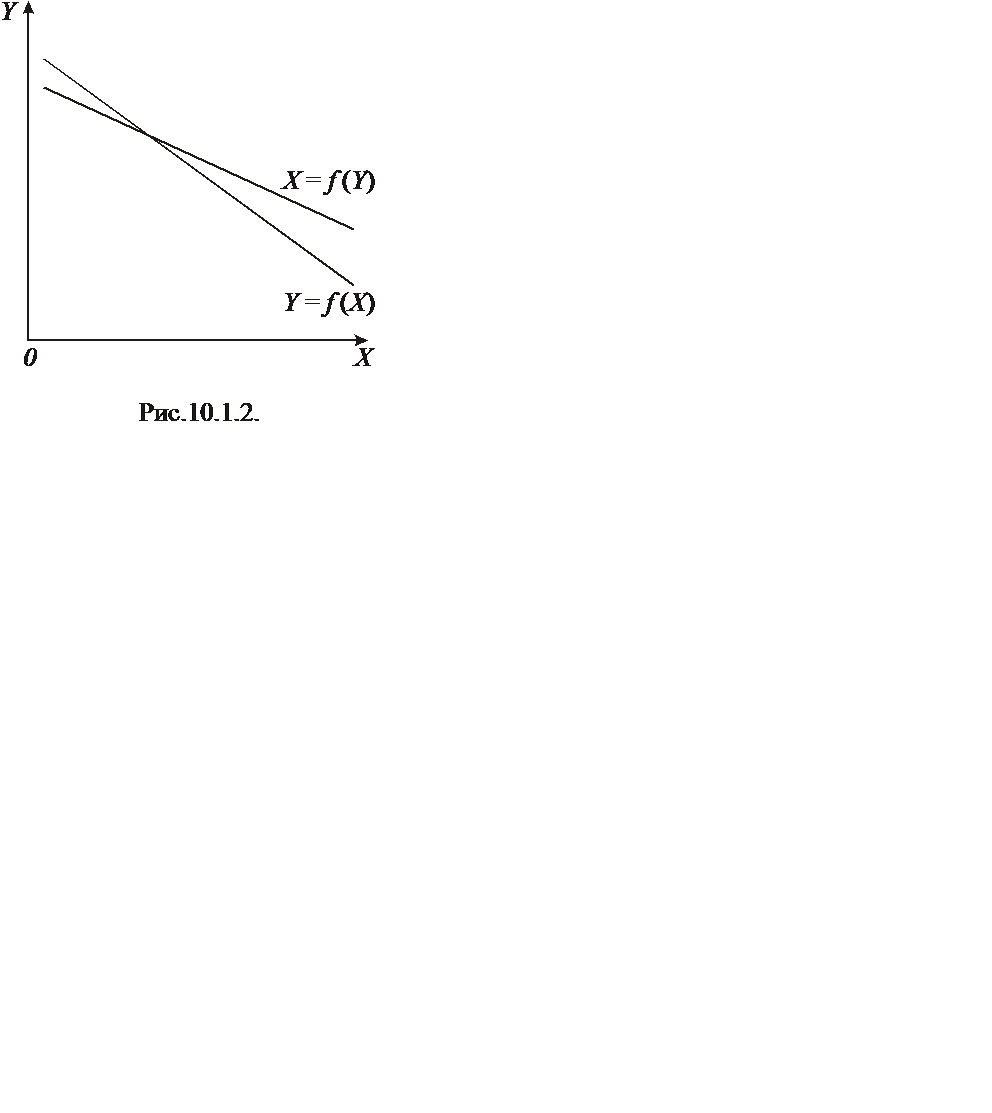Графически:

т.е. чем меньше связь между изучаемыми признаками, тем больше различие между направлениями линий регрессии. В случае полного отсутствия связи (признаки варьируют независимо) теоретические линии регрессии оказываются взаимно перпендикулярными, идущими параллельно осям координат (поскольку b_x_/_y = b_y_/_x = 0).

Соответствующая этой зависимости теоретическая линия регрессии х/у) не совпадает с линией регрессии у/х, и в этом проявляется специфика корреляционной связи. Чем меньше степень линейной связи, тем больше угол между линиями регрессии. При r = 0 линии регрессии х/у и у/х оказываются взаимно перпендикулярными и идущими параллельно осям координат. При строго функциональной связи (|r| = 1) линии регрессии сливаются в одну.

Если известно значение коэффициента корреляции r_xy, то значение коэффициента регрессии можно вычислить по формулам:

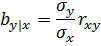
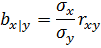
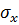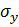где и - средние квадратичные отклонения для Х и У. Параметр 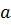в уравнении регрессии в этом случае будет определяться согласно выражениям:

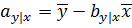
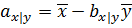
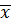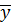где и – средние арифметические для признаков Х и У.

Коэффициент корреляции и оба коэффициента регрессии всегда имеют один знак.

Кроме того, полезно заметить, что коэффициент корреляции:

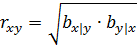
есть среднее геометрическое из коэффициентов регрессии.

⇐ Предыдущая 12