Лекция 6(8). РЕГРЕССИОННЫЙ АНАЛИЗ

Лекция 6(8)

РЕГРЕССИОННЫЙ АНАЛИЗ

Корреляционный анализ дает возможность получить общее представление о наличии связи между признаками и степень тесноты этой связи. Следующим этапом является определение количественной зависимости между величинами признаков (случайных величин), осуществляемое с помощью регрессионного анализа.

Для выяснения сути регрессионного анализа воспользуемся условным примером, соответствующим корреляционной модели.

Пример: Имеется следующий ряд сопряженных значений признаков ( Х – максимальная гигроскопичность %, У – удельная теплота смачивания, кал/г)

X_i

Y_i

Для каждого отдельного значения Х_i можно вычислить среднее значение У_i₍_x₎ второго признака.

X_i
У_i₍_x₎			3,5

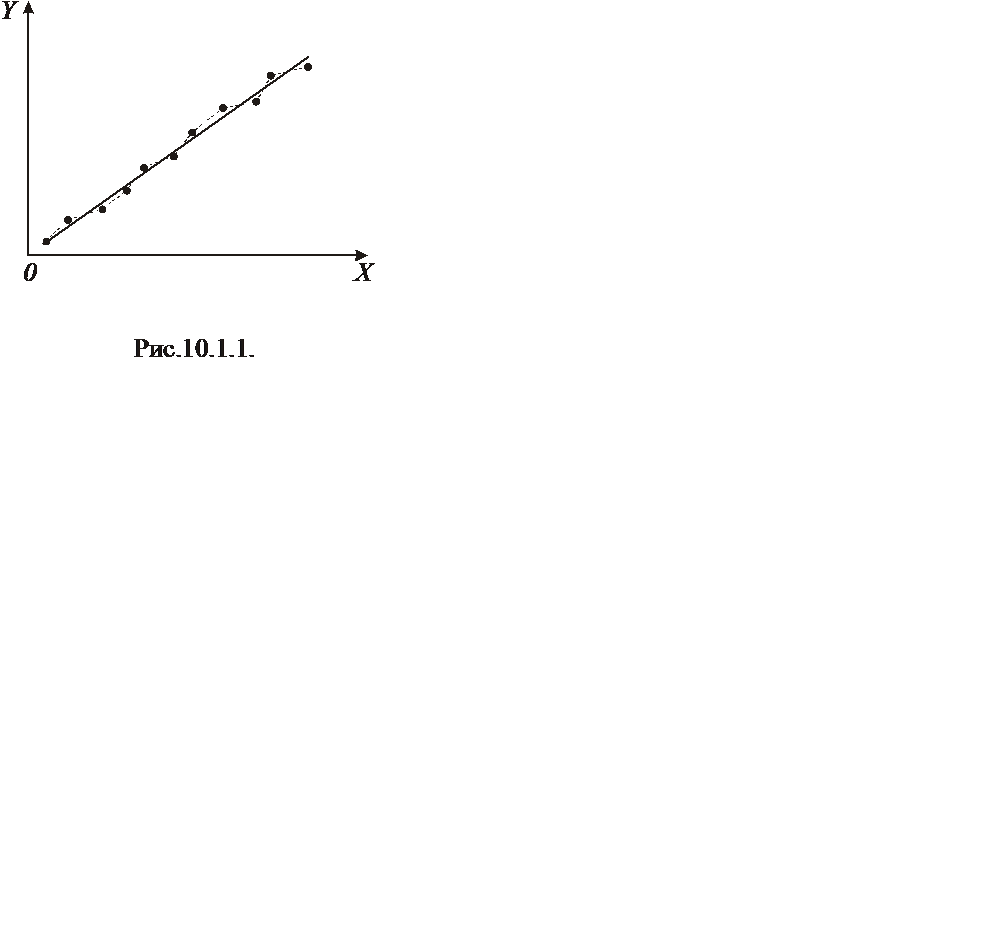Каждое значение У_i₍_x₎ представляет собой лишь выборочную оценку того генерального среднего 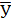_i₍_x₎, которое соответствует данной величине X_i, в результате чего в эмпирической линии регрессии наблюдаются изломы, имеющие случайный характер. За случайными флуктуациями (изломами) скрывается реально существующая связь генеральных средних У_i₍_x₎ и величин X_i. В данном примере связь прямолинейная, которую можно выразить в виде: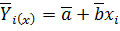

где 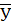_i₍_x₎ – генеральное среднее значение признака у_i при данном значении х_i, а и – некоторые постоянные коэффициенты, именуемые параметрами уравнения регрессии (в данном случае эти параметры генеральные, что обозначено чертой).

Генеральные параметры в уравнении регрессии обычно также неизвестны, но для них можно найти выборочные оценки, что также является одной из главных задач регрессионного анализа.

Располагая вместо генеральных параметров их выборочными оценками, нельзя по уравнению регрессии вычислить генеральное среднее значение функции по известному аргументу. Такое уравнение позволяет найти лишь оценку этого генерального значения среднего при данной величине х_i. Поэтому более правильно записать:

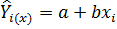
Линия, являющаяся графическим выражением уравнения регрессии, получила название теоретической линии регрессии одного признака по другому.

Для каждого сопряженного ряда величин Х и У обычно бывает возможно найти множество уравнений данного типа с несколько отличными параметрами, которые удовлетворяют условию, что сумма отклонений у_i от вычисленных для тех же значений х_i оценок равна нулю

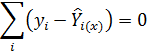
Но среди этих уравнений существует только одно, параметры которого имеют такие значения, при которых сумма квадратов отклонений у_i от имеет наименьшее значение:

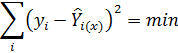
Способ отыскания оценок параметров, основанный на минимизации 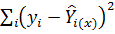получил название способа наименьших квадратов. Оценки, полученные этим способом, считаются наилучшими.

Коэффициент при аргументе 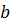получил название коэффициента регрессии. Он количественно характеризует изменение функции с изменением аргумента. Если (или 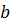) равен нулю, то функция от соответствующего аргумента не зависит (имеется в виду функция данного типа). Так предположив, что в предыдущем уравнении 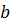=0, получим, что 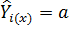при любых значениях х_i.

Выборочные оценки коэффициентов регрессии никогда не бывают в точности равны 0, даже если в генеральной совокупности связь между признаками отсутствует полностью. В связи с этим встает задача выяснить, насколько значимо полученный коэффициент регрессии отличен от 0 и, следовательно, можно ли утверждать, что связь между признаками реально существует.

Требования к исходным данным:

1. Случайные величины (признаки) х_i и у_i должны иметь нормальное распределение.

2. Результаты наблюдения должны быть независимы друг от друга

3. Величины условной дисперсии зависимой переменной при различных значениях независимой переменной должны быть одинаковы. (???)

Пропустить

12 Следующая ⇒