
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Доказать тождество: cos2x = 2cos2x – 1
№2. Доказать тождество: cos2x = 2cos2x – 1
Доказательство:
cos2x = cos2x – sin2x = cos2x – (1 - cos2x) = 2cos2x – 1
cos2x = 2cos2x – 1, что и требовалось доказать.
Если из полученного равенства выразить cos2x, то получим:
cos2x = 2cos2x – 1
cos2x+1 = 2cos2x
2cos2x = cos2x+1
cos2x = 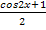 - еще одна формула понижения степени.
- еще одна формула понижения степени.
Таким образом, выполняя задания №1 и №2, доказывая тождества, получили еще два варианта формул двойного угла и как следствия из них- формулы понижения степени.
sin2x = 2sinxcosx; cos2x = cos2x – sin2x;
cos2x = 1 – 2sin2x; cos2x = 2cos2x – 1
sin2x = 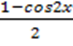 ; cos2x =
; cos2x = 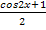
Рассмотрим примеры использования формул двойного аргумента.
Пример1. Вычислить:
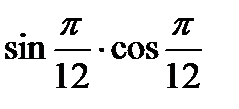
Решение:
a) 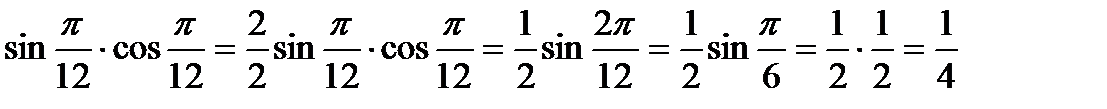
Пример 2. Вычислить::
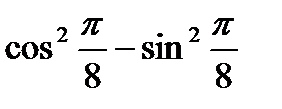
Решение:
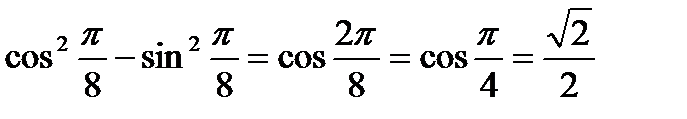
Пример 3. Вычислить:
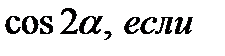
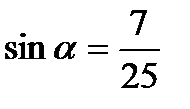 , 0< α <
, 0< α < 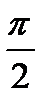
Решение:
cosα >0
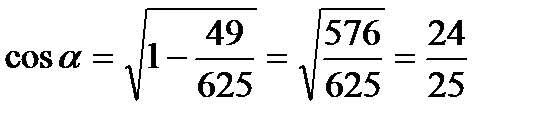
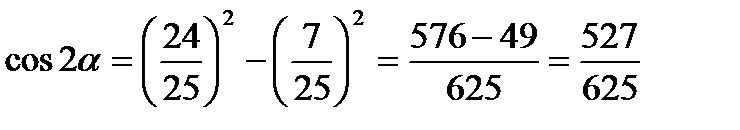
Самостоятельная работа:
Вариант 1
1. Заполните пропуски в равенствах так, чтоб они стали верными равенствами:
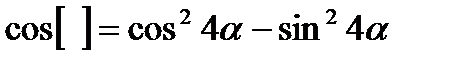 2.
2. 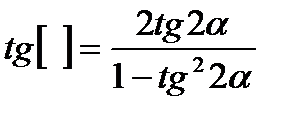 3. Упростите:
3. Упростите:
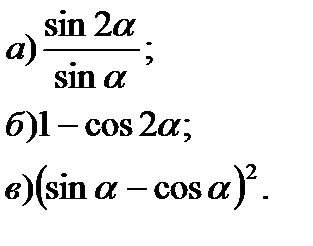 4. Вычислите: 4. Вычислите:
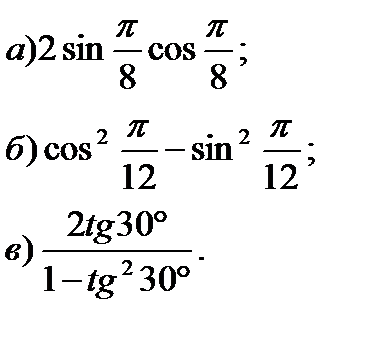
| Вариант 2
1. Заполните пропуски в равенствах так, чтоб они стали верными равенствами:
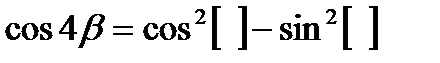 2.
2. 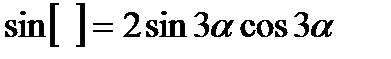  3. Упростите:
3. Упростите:
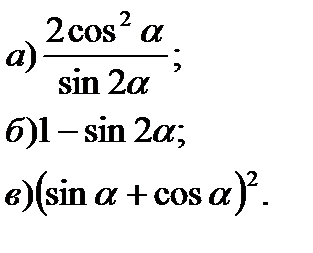 4. Вычислите:
4. Вычислите:
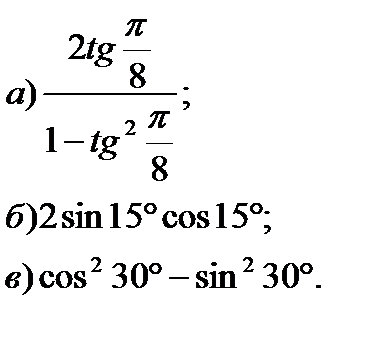
|
3. Контрольные вопросы:
1. Записать формулы двойного аргумента.
2. Найти ctg2x
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|