Алгоритм решения задач. Примеры решения задач

Алгоритм решения задач

Уравнение состояния (2.1) связывает между собой пять физических величин, которые характеризуют состояние газа 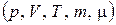и позволяет по заданным четырем найти пятую величину.

В общем случае алгоритм решения может быть такой. Из условий задачи определить, какие процессы происходят при переходе газа из начального состояния в конечное. Если газ последовательно совершает несколько различных процессов, целесообразно сделать схематический чертеж, на котором изобразить все процессы и обозначить параметры газа в начале и в конце каждого из них. Для начального и конечного состояния газа в каждом процессе следует записать уравнение Менделеева-Клапейрона для начального и конечного состояния газа в процессе или уравнение изопроцесса. Замкнуть полученную систему, решить ее и проанализировать полученный результат.

Если надо определить некоторый неизвестный параметр в смеси идеальных газов, не реагирующих между собой, тогда для решения целесообразно использовать уравнение состояния идеального газа, основное уравнение кинетической теории газа и закон Дальтона. Все описанные выше действия надо выполнить для каждой компоненты смеси отдельно, а результирующее давление смеси определить с помощью закона Дальтона.

Примеры решения задач

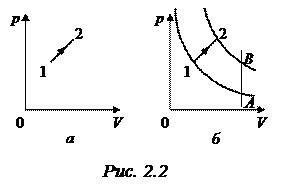Задача 2.1.В координатах р, V (рис. 2.2 а) изображён график зависимости давления р от объема V при переходе идеального газа из состояния 1 в состояние 2. Как изменялась температура в этом процессе?

Решение. Проведем две изотермы так, что одна из них пройдет через точку 1, а вторая – через точку 2 (рис. 2.2 б). Обозначим через Т₁ температуру, соответствующую первой изотерме, Т₂ – второй изотерме. Чтобы выяснить, какая из этих температур выше, проведем произвольную изохору, пересекающую изотермы в точках А и В. При постоянном объеме, согласно закону Шарля, р/Т =
= const. Следовательно,

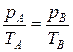где р_А, р_В – давление газа в состояниях А и В соответственно; Т_А, T_В – температура в этих состояниях. Отсюда находим

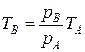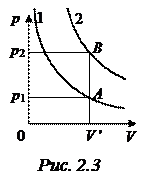Но, как видно из рис. 2.2 б, р_В > р_А. Следовательно, Т_В > Т_А, т. е. для газа данной массы большему давлению соответствует бóльшая температура. Таким образом, мы приходим к выводу, что изотерма, проходящая через точку 2, соответствует более высокой температуре, чем изотерма, проходящая через точку 1, т. е. Т₂ > Т₁. Значит, температура газа при переходе из состояния 1 в состояние 2 увеличилась.

Задача 2.2. На рис. 2.3 изображены две изотермы для двух различных газов, имеющих одинаковые массу и температуру. Сравнить молярные массы этих газов.

Решение. По условию задачи газы имеют одинаковую массу m и одинаковую температуру Т. Рассмотрим на различных изотермах два состояния А и В, которым соответствует один и тот же объем 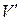. Запишем уравнение Менделеева-Клапейрона для этих состояний:

, ,

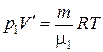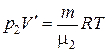где μ₁, μ₂ – молярные массы первого и второго газов соответственно.

Разделив почленно первое уравнение на второе, получим 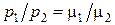, откуда

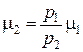Учитывая, что 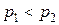, приходим к выводу, что 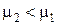, т. е. изотерма 2 соответствует газу, имеющему меньшую молярную массу, чем газ, которому соответствует изотерма 1.

Как показано при решении этой задачи, изотермы, соответствующие одной и той же температуре, но различным газам, могут не совпадать вследствие различия масс и молярных масс газов, так как от этих величин зависит константа, входящая в математическое выражение закона Бойля-Мариотта (2.3). В самом деле, это выражение, как отмечалось выше, является частным случаем уравнения Менделеева-Клапейрона, поэтому

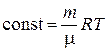Отсюда видно, что константа имеет различные значения при различных m, μ и Т. Чем больше числовое значение этой константы, тем выше и правее будет располагаться соответствующая изотерма.

Задача 2.3. График зависимости давления р идеального газа от его температуры Т в некотором процессе изображен на рис. 2.4 а. Определить, сжимался или расширялся газ при переходе из состояния 1 в состояние 2.

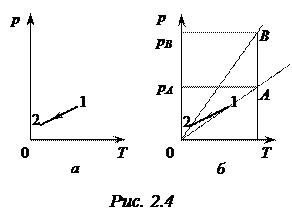Решение. Используем прием, аналогичный примененному при решении предыдущей задачи. Проведем две изохоры, одна из которых проходит через точку 1, вторая – через точку 2 (рис. 2.4 б), т. е. первая изохора соответствует объему V₁ в состоянии 1, вторая – объему V₂ в состоянии 2. Проведем произвольную изотерму, пересекающую изохоры в точках А и В. Согласно закону Бойля-Мариотта, при постоянной температуре pV = const. Следовательно,

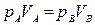где р_А, V_A – давление и объем газа в состоянии А; р_B, V_B – в состоянии В.

Отсюда

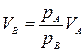а так как р_A < р_B, то V_B < V_А, т. е. для газа данной массы большему давлению соответствует меньший объем. Таким образом, мы приходим к выводу, что
V₂ < V₁, т. е. при переходе из состояния 1 в состояние 2 газ сжимался.

Задача 2.4. Начертить графики изотермического расширения идеального газа данной массы в координатах р, V; Т, V; ρ, р; ρ, Т, где р, V, Т и ρ – соответственно давление, объем, температура и плотность газа.

Решение. Как отмечалось выше, при изотермическом процессе (m = const, T = const) справедлив закон Бойля-Мариотта: pV = const. График этой зависимости (изотерма) в координатах р, V показан на рис. 2.5 а. В координатах Т, V эта изотерма дана на рис. 2.5 б.

Найдем теперь зависимость плотности идеального газа от давления и температуры. Как известно, плотность 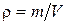, для ее нахождения разделим обе части уравнения Менделеева-Клапейрона 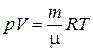на объем, получим выражение для плотности идеального газа:

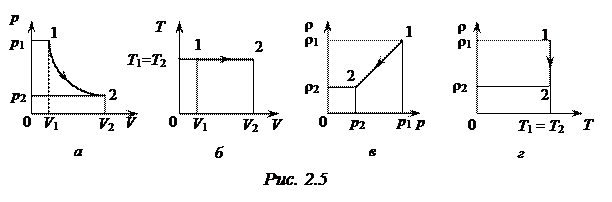
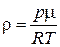Отсюда видно, что при изотермическом расширении газа его плотность прямо пропорциональна давлению. Учитывая это, начертим графики в координатах ρ, р и ρ, Т (рис. 2.5 в, г соответственно).

Задача 2.5. Газ нагревается в открытом сосуде при нормальном давлении от температуры 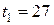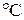до 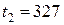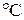. Найти приращение концентрации молекул в сосуде.

Решение. В связи с тем, что газ нагревается в открытом сосуде, давление газа остается постоянным, т. е.:

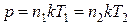, (1)

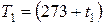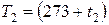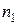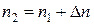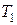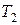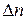где К, К – абсолютные температуры; и – концентрации молекул при температурах и ; –приращение концентрации.

Из (1) следует

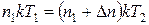
или

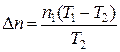. (2)

Согласно (1) 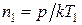, тогда (2) принимает вид

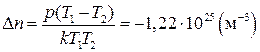т. е. концентрация газа уменьшается.

Задача 2.6.Найти молярную массу смеси газов, считая, что она состоит по массе из одной части кислорода и трех частей азота.

Решение. Если мы имеем смесь газов, то необходимо рассматривать так называемую молярную массу смеси 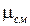, которая должна удовлетворять уравнению состояния:

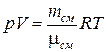, (1)

где 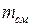– масса смеси.

Но тот же самый закон мы можем записать для каждой компоненты смеси отдельно:

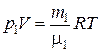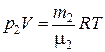, , (2)

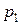где и 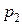– парциальные давления каждой компоненты.

Для смеси газов выполняется закон Дальтона (2.7):

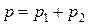Подставив в последнее уравнение 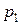и 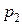из уравнения (2), получим:

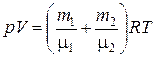. (3)

Сравнивая (1) и (3) и учитывая, что 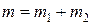, для молярной массы смеси имеем:

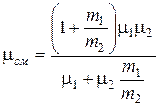Подставив числовые значения ( 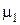= 0,032 кг/моль, 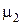= 0,028 кг/моль и 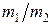= 1/3), получим 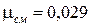кг/моль. Полученное числовое значение приблизительно равно молярной массе воздуха, что не удивительно, поскольку воздух на 98,6 % состоит из азота и кислорода.

Задача 2.7.В баллоне объемом 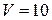л находится гелий под давлением 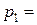1 МПа, при температуре 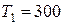К. После того, как из баллона выпустили 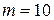г гелия, температура в баллоне понизилась до 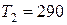К. Определить давление 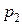гелия, оставшегося в баллоне.

Решение. Применив уравнение Менделеева-Клапейрона к конечному состоянию газа, найдем давление:

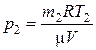, (1)

где 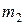– масса гелия в баллоне в конечном состоянии.

Массу 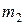гелия выразим через массу 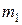, которая соответствует начальному состоянию, и массу 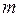гелия, которую выпустили из баллона

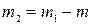. (2)

Массу 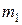гелия найдем из уравнения Менделеева-Клапейрона, применив его к начальному состоянию:

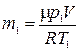Подставим последнее выражение для массы 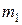в уравнение (2), а потом 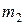в (1), получим:

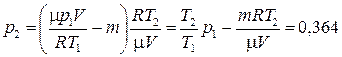(МПа).

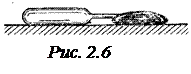Задача 2.8.Сколько ртути войдет в стеклянный баллончик объемом 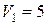см³, нагретый до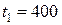 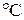при его охлаждении до 16 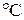? Плотность ртути при 16 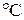равняется 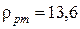г/см³ (рис. 2.6).

Решение. Ртуть входит в баллон при его охлаждении, поскольку при изобарном процессе с понижением температуры объем воздуха в баллоне должен уменьшиться. Обозначим через 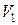начальный объем воздуха в баллоне, после охлаждения объем воздуха уменьшится до 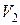, поскольку часть объема баллона займет ртуть. Ртуть втягивается и поддерживает давление воздуха внутри баллона постоянным.

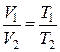В баллон войдет ртуть массы

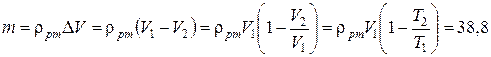(г).

Задача 2.9.Воздух находится в цилиндре под свободно перемещающимся поршнем. Поршень находится на высоте 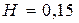м. Цилиндр нагревается от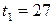 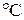до 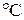. Масса поршня 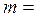3 кг, площадь 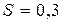дм². Определить работу, которую совершает воздух при расширении, передвигая поршень.

Решение. Поршень находится в равновесии, если 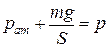, где 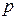– давление воздуха снизу на поршень (рис. 2.7). Давление постоянное (поскольку поршень свободно передвигается), поэтому можно применить закон Гей-Люссака

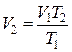где V₁– объем воздуха в цилиндре при температуре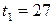

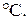
Работа

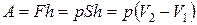
или

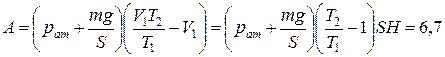(Дж).

⇐ Предыдущая 12