Контакты

Случайная статья

Степень с целым и дробным показателем

⇐ ПредыдущаяСтр 2 из 2

Степень с целым и дробным показателем

Имеют место следующие тождества:

1) ;

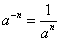2) ;

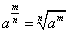3) .

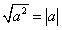Пример 2. Найти значение выражения

.

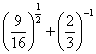Решение. Освободимся от отрицательного показателя и упростим исходное выражение:

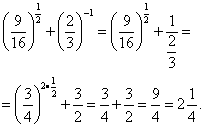
Пример 3. Найти значение выражения

.

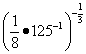Решение. Освободимся от отрицательных показателей и упростим исходное выражение:

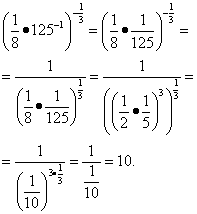
Пример 4. Найти значение выражения

.

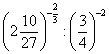Решение. Освободимся от отрицательных показателей и упростим исходное выражение:

.

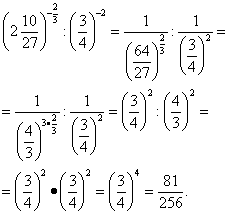
Преобразования арифметических корней.

1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: 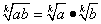, где 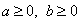(правило извлечения корня из произведения).

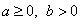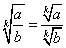2. Если , то (правило извлечения корня из дроби).

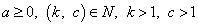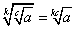3. Если , то (правило извлечения корня из корня).

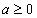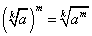4. Если , то (правило возведения корня в степень).

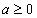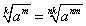5. Если , то , где 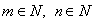, т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.

6. Если 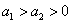, то 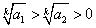, т. е. большему положительному подкоренному выражению соответствует и большее значение корня.

7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:

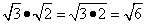(правило умножения корней),

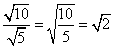(правило деления корней),

.

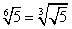8. Правило вынесения множителя из-под знака корня. При .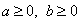

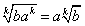9. Обратная задача - внесение множителя под знак корня. Например,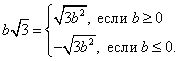

10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.

а) 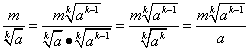, так как .

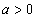Например, .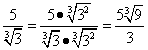

б)

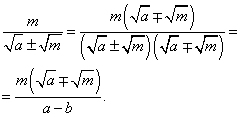
Например,

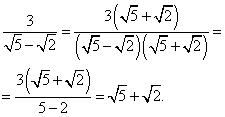
в)

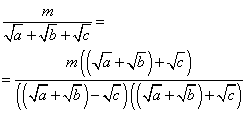
и т. д.

11. Применение формул сокращённого умножения к действиям с арифметическими корнями:

1) ;

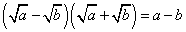2) ;

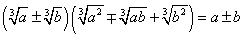3)

⇐ Предыдущая 12

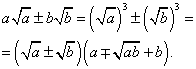
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.