
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Схема вычисления производной функции
Схема вычисления производной функции
1. Найти приращение функции на отрезке [x; x+Δx]:
∆y=y(x+∆x)-y(x)
1. Разделить приращение функции на приращение аргумента:
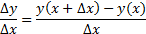
1. Найти предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
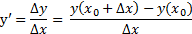
Пример 4.
Вычислить производную функции y=x2
Решение: Используем схему вычисления производной по действиям:
1. ∆y=y(x+∆x)-y(x)= (х+∆х)²-х²= х²+2х·∆х+ ∆х²-х²= 2х·∆х+ ∆х²
2. 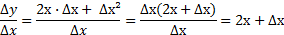
3. 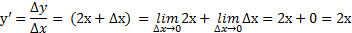
Ответ: y’=2x.
Физический смысл производной: если положение точки при её движении задаётся функцией пути S(t), где t – время движения, то производная функции S есть мгновенная скорость движения в момент времени t: v(t)=S’(t).
Таким образом, скорость – есть производная от пути по времени.
Пример 5.
Точка движется по закону s(t)=1-2t. Найдите среднюю скорость движения за промежуток времени от t=0,8 до t=1.
Решение:
найдем ∆t= 1-0,8=0,2
S(0,8)= 1-2·0,8= -0,6=S(t)
S(1)= 1-2·1= -1=S(t+∆t)
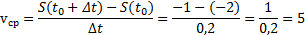 .
.
Ответ: 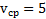 .
.
Необходимое и достаточное условие дифференцируемости
Теорема 1. Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.
Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx.
Просмотрите видео : https://youtu.be/fiQv1OgJMK8
Домашнее задание:§44, решить на стр.235, №776, №780(1,2), просмотреть видео по ссылке
https://youtu.be/QygmvlwtyXQ
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|