Перечень вопросов, рассматриваемых в теме

Стр 1 из 2Следующая ⇒

Тема. Производная

Учебная дисциплина: алгебра и начала анализа

Дата: 15 ноября 2021 г.

Класс. 11

Учитель: Данилова А.Ф.

Перечень вопросов, рассматриваемых в теме

1) Определение производной;

2) Физический смысл производной;

2) Приращение функции;

3) Скорость материальной точки в заданный момент времени по данному закону движения.

ЗАПИШИТЕ

Семнадцатое ноября

Классная работа

Тема. Производная .ЕЕ физический смысл.

ПРОЧТИТЕ и СДЕЛАЙТЕ КОНСПЕКТ,

Изучая поведение функции y=f(x) около конкретной точки x₀, важно знать, как меняется значение функции при изменении значения аргумента. Для этого используют понятия приращений аргумента и функции

Пусть функция y=f(x) определена в точках x₀ и x₁. Разность x₁−x₀ называют приращением аргумента(при переходе от точки x₀ к точке x₁), а разность f(x₁)-f(x₀) называют приращением функции.

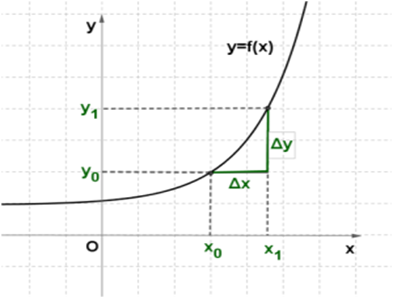
Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита "дельта"; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.

Итак, x₁-x₀=Δx, значит, x₁=x₀+Δx.

f(x₁)-f(x₀)=Δy, значит,

Δy=f(x0+Δx)-f(x0). (1)

Нельзя истолковывать термин "приращение" как "прирост".

Примеры и разбор решения заданий

Пример 1.Найдем приращение Δx и Δf в точке x_0,если f(x)= x², x₀=2 и х=1,9

Решение:

Δx= x₁−x₀=1,9-2=-0,1

Δf= f(1,9) –f(2)=1,9²-2²=-0,39

Ответ: Δx=-0,1; Δf =-0,39

Пример 2.Найдем приращение Δx и Δf в точке x_0,если f(x)= x², x₀=2 и х=2,1

Решение:

Δx= x₁−x₀=2,1-2=0,1

Δf= f(1,9) –f(2)=2,1²-2²=0,41

Ответ: Δx=0,1; Δf =0,41

Пример 3.Найдем приращение Δf функции 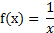в точке x₀,если приращение аргумента равно x₀.

Решение:

находим:

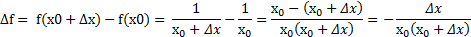Ответ: .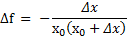

С помощью введенных обозначений приращений удобно также выражать среднюю скорость движения за промежуток времени [t₀; t₀+∆t]. Если точка движется по прямой и известна ее координата x(t), то

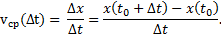
Эта формула верна и для ∆t<0 (для промежутка [t₀+∆t; t₀]).

Аналогично выражение 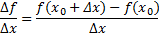называют средней скорость изменения функции на промежутке с концами х₀ и х₀+∆х.

Определение.Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

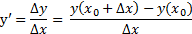
Обозначение: y’ или f’(x)

Если функция f(x) имеет производную в точке х, то эта функция называется дифференцируемой в этой точке. Если функция f(x) имеет производную в каждой точке некоторого промежутка, то эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.

12 Следующая ⇒