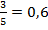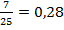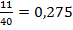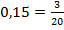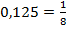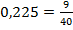- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение
Тема урока Действительные числа. Бесконечно убывающая геометрическая прогрессия.
1. Устная работа
2. Объяснение темы «Действительные числа»
1. Определение иррационального числа
2. Множество действительных чисел
3. Действия с бесконечными десятичными дробями
4. Модуль действительного числа
3. Решение тренировочных упражнений из учебникана закрепление темы
4.Объяснение темы «Бесконечно убывающая геометрическая прогрессия»
1. Геометрическая прогрессия (повторение)
2. Основные формулы геометрической прогрессии (повторение)
3. Бесконечно убывающая геометрическая прогрессия
4. Решение ключевой задачи №1
5. Формула суммы бесконечно убывающей геометрической прогрессии
6. Решение задач на закрепление
5. Решение тренировочных упражнений на закрепление темы
Ход урока
Устная работа
| Переведите в десятичную дробь: 1)
2)
3)
| Переведите в обыкновенную дробь: 1)
2)
3) | |
2. Объяснение темы «Действительные числа»:
1. Определение иррационального числа
Определение
Иррациональным числом называется бесконечная десятичная непериодическая дробь.
Иррациональные числа, как и рациональные, могут быть положительными и отрицательными.
Например, число 0,123456…., в котором после запятой записаны подряд все натуральные числа, является положительным иррациональным числом. Число -5, 246810…., в которм после запятой записаны подряд все четные числа, является отрицательным иррациональным числом.
Числа 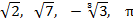 также являются иррациональными, так как можно доказать, что они могут быть представлены в виде бесконечных десятичных непериодических дробей.
также являются иррациональными, так как можно доказать, что они могут быть представлены в виде бесконечных десятичных непериодических дробей.
Множество действительных чисел
Рациональные и иррациональные числа образуют множество действительных чисел.
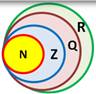
Действия с бесконечными десятичными дробями.
Известно как выполняются действия над конечными десятичными дробями. Арифметические операции над действительными числами, т.е. бесконечными десятичными дробями, заменяются операциями над их приближениями.
Например,вычислим приближенные значения 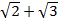
Решение:
Воспользуемся калькулятором и найдем значения 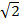 и
и 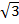
Имеем 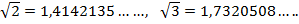
Найдем 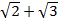 с точностью до единицы
с точностью до единицы
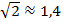 и
и 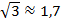 , тогда
, тогда 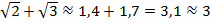
Найдем 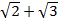 с точностью до одной десятой
с точностью до одной десятой
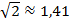 и
и 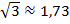 , тогда
, тогда 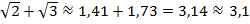
Найдем 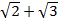 с точностью до одной сотой
с точностью до одной сотой
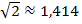 и
и 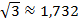 , тогда
, тогда 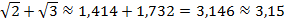
Анальгично, вычисляя произведение 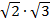 с точностью до 0,1, получаем
с точностью до 0,1, получаем
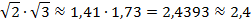
Все основные действия над рациональными числами сохраняются и для действительных чисел (переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и т.д.).
4. Модуль действительного числа
Определение.
Модуль действительного числа 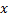 обозначается
обозначается 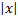 и определяется так же, как и модуль рационального числа:
и определяется так же, как и модуль рационального числа:
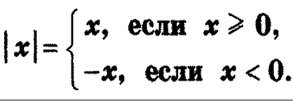
2. Решение тренировочных упражнений
Выяснить, каким числом (рациональным или иррациональным) является числовое значение выражения:
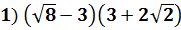
Решение: Перемножим скобки
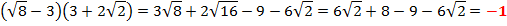
Ответ: является рациональным числом
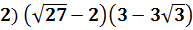
Решение: Перемножим скобки
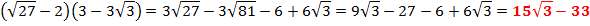
Ответ: является иррациональным числом
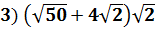
Решение: Раскроем скобки (распределительный закон)
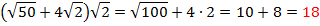
Ответ: является рациональным числом
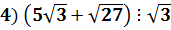
Решение: Раскроем скобки (распределительный закон)
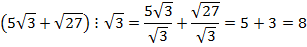
Ответ: является рациональным числом
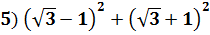
Решение: Раскроем скобки (формулы сокращенного умножения)
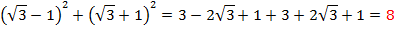
Ответ: является рациональным числом
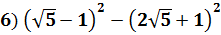
Решение: Раскроем скобки (формулы сокращенного умножения)
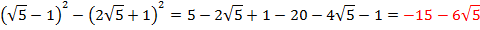
Ответ: является иррациональным числом
Вычислить:
1) 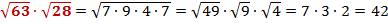
2) 
3) 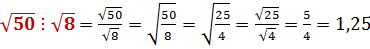
4) 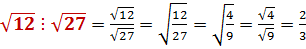
Объяснение темы «Бесконечно убывающая геометрическая прогрессия»:
Геометрической прогрессией называется такая числовая последовательность 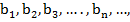 что для всех натуральных
что для всех натуральных 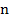 выполняется равенство
выполняется равенство
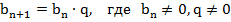
Например, 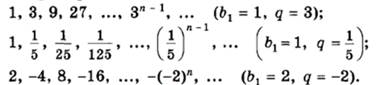
1. Формула -го члена геометрической прогрессии:
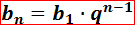
2. Формула суммы 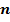 первых членовгеометрической прогрессии:
первых членовгеометрической прогрессии:
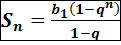 , если
, если 
3. Если  , то
, то 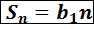
Среди геометрических прогрессий особый интерес представляют бесконечно убывающие геометрические прогрессии.
Пример. Рассмотрим квадраты, изображенные на рисунке. Сторона первого квадрата равна 1, сторона второго равна 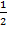 , соторна третьего
, соторна третьего  и т.д.
и т.д. 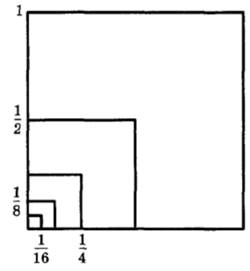
Таким образом, стороны квадратов образуют геометрическую пргрессию со знаменателем 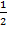 :
:
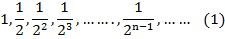
Площади этих квадратов образуют геометрическую прогрессию со знаменателем 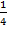
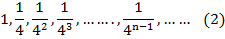
Из рисунка видно, что стороны квадратов и их площади с возрастанием номера 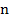 становятся все меньше, приближаясь к нулю. Поэтому каждая из прогрессий (1) и (2) называется бесконечно убывающей.
становятся все меньше, приближаясь к нулю. Поэтому каждая из прогрессий (1) и (2) называется бесконечно убывающей.
Рассмотрим геометрическую прогрессию
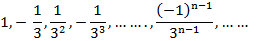
Знаменатель этой прогрессии 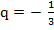 , а ее члены
, а ее члены 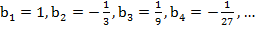
С возрастанием номера 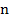 члены этой прогрессии приближаются к нулю. Эту прогрессию так же называют бесконечно убывающей. Ометим, что модуль ее знаменателя меньше единицы:
члены этой прогрессии приближаются к нулю. Эту прогрессию так же называют бесконечно убывающей. Ометим, что модуль ее знаменателя меньше единицы: 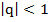
Определение.
Геометрическая прогрессия называется бесконечно убывающей, если модуль ее знаменателя меньше единицы.
3. Решение ключевой задачи
Задача №1.
Доказать, что геометрическая прогрессия, заданная формулой -го члена 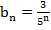 , является бесконечно убывающей.
, является бесконечно убывающей.
Решение:
1. Найдем первый и второй члены заданной геометрической прогрессии:
2. 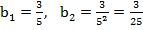
3. Найдем знаменатель геометрической прогрессии:
4. 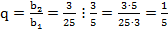
Так как модуль полученного знаменателя меньше единицы, т.е. 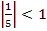 , то по определению данная геометрическая прогрессия является бесконечно убывающей.
, то по определению данная геометрическая прогрессия является бесконечно убывающей.
Формула суммы бесконечно убывающей геометрической прогрессии
Рассмотрим квадрат состороной равной единице. Отметим штриховкой его половину, затем половину оставшейся части и т.д. Площади заштрихованных прямоугольников образуют бесконечно убывающую геометрическую прогрессию
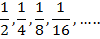
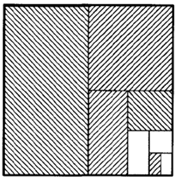
Если заштриховать все полученные таким образом прямоугольники, тоштриховкой покроется весь квадрат. Естественно считать, что сумма площадей всех заштрихованных прямоугольников равна единице, т.е.
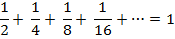
Выведем формулу суммы бесконечно убывающей геометрической прогрессии с помощью формулысуммы 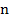 первых членовгеометрической прогрессии
первых членовгеометрической прогрессии
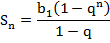
1) Запишем ее так: 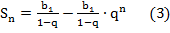
2) Так как 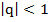 , то
, то 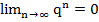 ,
, 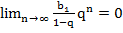 ,
,
поэтому 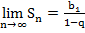
3) Таким образом, сумма S бесконечно убывающей геометрической прогрессии вычисляется по формуле:
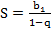 (4)
(4)
4) Из формулы (4) при 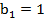 получаем
получаем 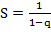 .
.
5) Это равенство обычно записывают так:
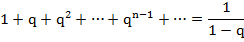
Заметим, что это равенство справедливо при 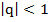 , в частности при
, в частности при 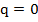
Решение ключевых задач
Задача №2.Найти сумму бесконечно убывающей геометрической прогрессии
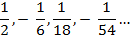
Решение:
1. Выпишем 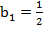 и
и 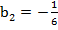 и найдем
и найдем 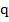 :
:
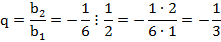
2. 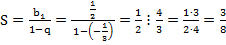
Задача №3.Найти сумму бесконечно убывающей геометрической прогрессии, если 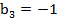 ,
, 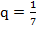
Решение:
1. Необходимо найти 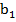 , поэтому воспользуемся формулой
, поэтому воспользуемся формулой 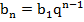 , тогда
, тогда 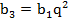
2. Подставим данные, 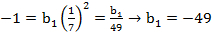
3. 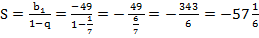
Задача №4.Записать бесконечную периодическую десятичную дробь 1,1(3) в виде обыкновенной.
Решение:
1. Число 1,1(3) можно записать в виде суммы 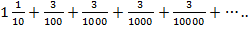
Сумма слагаемых, начиная со второго, является суммой 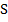 бесконечно убывающей геометрической прогрессии.
бесконечно убывающей геометрической прогрессии.
2. Тогда 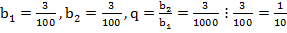
3. Получаем, 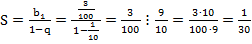
4. Учитывая исходные данные, получаем 1,1(3) 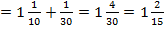
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|