
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Целая, четная
Стр 1 из 2Следующая ⇒
Степенная функция. Свойства и график
Функция 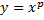 , где p- известная степень. В зависимости от степени, функция принимает различный вид.
, где p- известная степень. В зависимости от степени, функция принимает различный вид.
Вспомним, какие бывают числа:
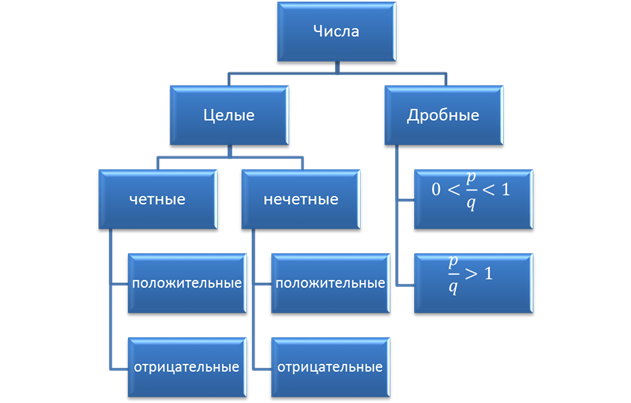
| Степень | ||
Целая, четная
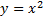
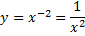
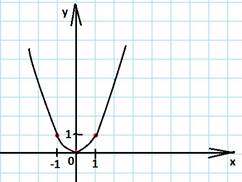

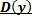 Область определения функции — это множество всех значений аргумента (переменной x).
Отвечает на вопрос: Каким может быть значение х
Область определения функции — это множество всех значений аргумента (переменной x).
Отвечает на вопрос: Каким может быть значение х
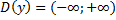
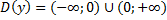
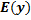 Множество значений функции — множество всех значений, которые функция принимает на области определения.
Отвечает на вопрос: Каким может быть значение y
Множество значений функции — множество всех значений, которые функция принимает на области определения.
Отвечает на вопрос: Каким может быть значение y
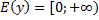
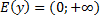
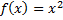
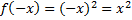

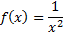
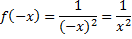

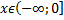 – функция возрастает
– функция возрастает
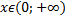 – функция убывает
– функция убывает
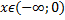 – функция возрастает
– функция возрастает
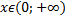 – функция убывает
– функция убывает
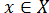 .
2). Функция f(x), определённая на множестве X, называется ограниченной снизу числом А, если f(x)≥A для любого.
3). Функция, ограниченная как сверху, так и снизу, называется просто ограниченная функция
.
2). Функция f(x), определённая на множестве X, называется ограниченной снизу числом А, если f(x)≥A для любого.
3). Функция, ограниченная как сверху, так и снизу, называется просто ограниченная функция
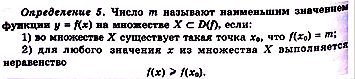
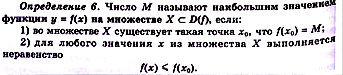 Свойства(стр75):
1) Если у функции существует
Свойства(стр75):
1) Если у функции существует 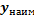 , то она ограничена снизу
2) Если у функции существует
, то она ограничена снизу
2) Если у функции существует 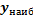 , то она ограничена сверху
3) Если функция не ограничена сверху, то у нее нет
, то она ограничена сверху
3) Если функция не ограничена сверху, то у нее нет 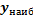 4) Если функция не ограничена сверху, то у нее нет
4) Если функция не ограничена сверху, то у нее нет 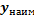
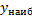 2). Т.к.
2). Т.к. 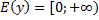 , но наименьшим значением будет 0.
, но наименьшим значением будет 0.
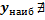
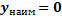
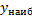 2). Т.к.
2). Т.к. 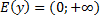 , но наименьшего значения, тоже не будет
, но наименьшего значения, тоже не будет
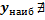
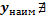


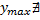
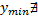
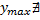
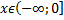 – вогнута
– вогнута
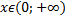 – вогнута
– вогнута
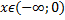 – вогнута
– вогнута
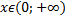 – вогнута
– вогнута