
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Свойства высоты треугольника
⇐ ПредыдущаяСтр 2 из 2
Свойства высоты треугольника
ü Высоты треугольника обратно пропорциональны соответствующим сторонам.
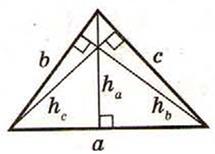
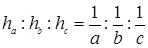
ü Высота треугольника не больше биссектрисы и медианы треугольника, проведенных из одной вершины.

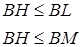
ü Сумма расстояний от оснований двух высот треугольника к середине его третьей стороны равна третьей стороне.
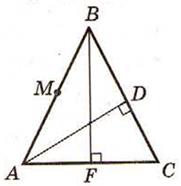
Если АМ = МВ, BF  AC, AD
AC, AD  BC,
BC,
то MF + MD = AB
ü Прямые, содержащие высоты треугольника, пересекаются в одной точке (ортоцентре треугольника).
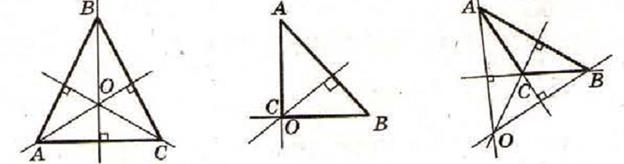
ü Если AD, BE, CF – высоты треугольника ABC, О – точка пересечения этих высот или их продолжений, то

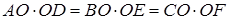
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|