Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

ВК – медиана ,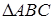

если К – середина АС (АК = КС)

Всего в треугольнике можно провести три медианы (по одной из каждой вершины).

Все медианы лежат внутри треугольника.

Свойства медиан треугольника:

ü Медианы треугольника пересекаются в одной точке – центре тяжести треугольника и делятся этой точкой в отношении 2 : 1, считая от вершины угла.

                                                           АО = 2ОЕ

                                                           ВО = 2OF

                                                           СО = 2OD

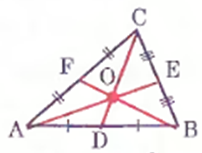
ü Медиана треугольника не меньше высоты и биссектрисы треугольника, которые проведены из одной вершины.

                                                           ВМ ≥ BL

                                                           BM ≥ BH

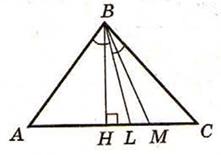
ü Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.



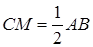
ü Длины медианы треугольника m_a, m_b, m_c связаны со сторонами a, b, c треугольника отношением: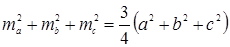

    Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

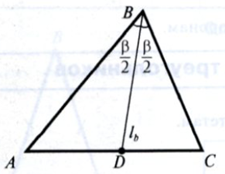
                                             BD – биссектриса треугольника



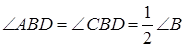
    Всего в треугольнике можно провести три биссектрисы (по одной из каждой вершины).

    Все биссектрисы лежат внутри треугольника.

Свойства биссектрисы треугольника

ü 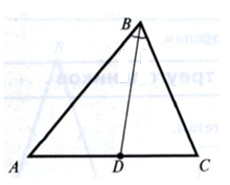Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

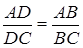
ü Биссектриса треугольника не меньше высоты треугольника и не больше медианы треугольника, которые проведены из одной вершины



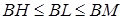
ü Биссектрисы внутреннего и смежного с ним внешнего угла треугольника перпендикулярны.

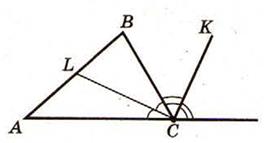
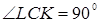
ü Биссектриса внешнего угла неравнобедренного треугольника пересекает продолжение противоположной стороны в точке, удаленной от концов стороны на расстояниях, пропорциональных двум другим сторонам



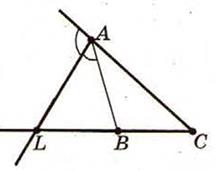
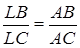
ü 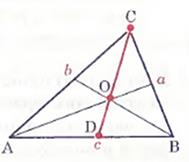Точка пересечения биссектрис делит биссектрису угла С в отношении 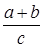, считая от вершины.



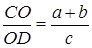
    Высота треугольника – перпендикуляр, проведенный из вершины к прямой, которая содержит противолежащую сторону треугольника.

                                                  BD – высота,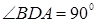



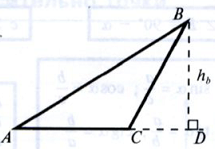
                                                    BD – высота,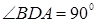



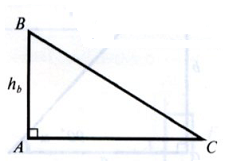
                                                BА – высота,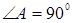

    Всего в треугольнике можно провести три высоты (по одной из каждой вершины).

12 Следующая ⇒