Хелпикс

Главная

Контакты

Случайная статья



Теорема синусов. Теорема косинусов. Соотношения между сторонами и углами в прямоугольном треугольнике. Площадь треугольника. Прямоугольный треугольник. Смежные углы. Вертикальные углы. Вертикальные углы равны. Параллелограмм. Трапеция. Метод координат. Ск

⇐ ПредыдущаяСтр 2 из 2


Теорема синусов

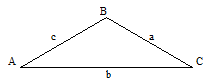
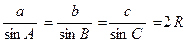
Теорема косинусов

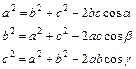
Площадь круга

Длина окружности

 

 

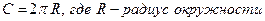
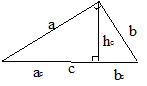
Соотношения между сторонами и углами в прямоугольном треугольнике

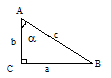
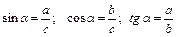
Площадь треугольника

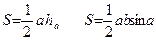
S = 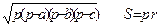,где p=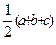

S = 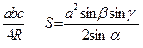,где r-радиус

впис. окруж. R – радиус опис. окруж.

Прямоугольный треугольник

 

 

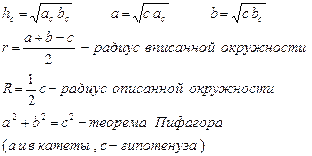
Смежные углы

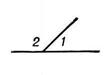
Вертикальные углы

 

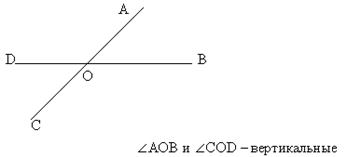
Вертикальные углы равны

Свойства биссектрисы внутреннего угла

 

 

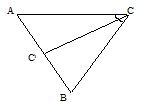
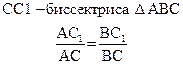
Параллелограмм

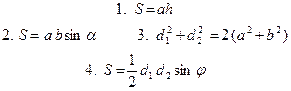
Ромб

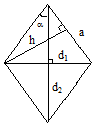
 Квадрат

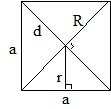
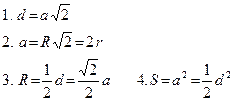
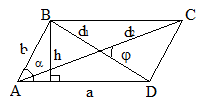
Трапеция

 

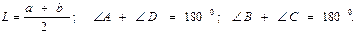
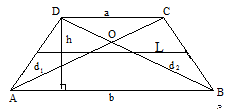S = lh =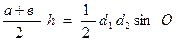

Метод координат

1) Пусть А(х1;у1), В(х2;у2), тогда координаты вектора .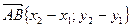

2) Пусть А(х1;у1), В(х2;у2), тогда длина вектора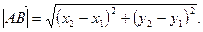

3) Пусть О(m;n) – середина отрезка АВ А(х1;у1), В(х2;у2), тогда

 m = 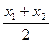 ; n = .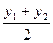

4) Пусть 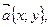тогда длина вектора

 

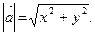
5) х2 + у2 = R2 - уравнение окружности с центром в точке (0;0) радиуса R.

 

6) (х – а)2 + (у-в)2 = R2 - уравнение окружности с центром в точке (a;в) радиуса R.

 

7) ах +ву +с = 0 – уравнение прямой.

 

Скалярное произведение векторов

1) Пусть 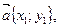b 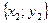, тогда скалярное произведение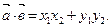

 2) Пусть 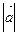-длина вектора 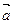, 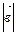длинавектора 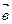, 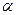- угол между векторами, тогдаскалярное произведение .

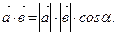3) 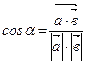- формула для нахожденияугла между векторами.

 

 

В1

1. Сформулируйте перекрёстное правило сравнения дробей.                                   

 

Сравни 21\33 и 9\22

 

 

2. Какой знак может иметь степень с отрицательным основанием?

Приведи примеры

n3,      n – основание

 

3. придумай задачу на пропорциональное деление какой-нибудь величины

 

 

В2

1. Какие величины называются прямо пропорциональными? Запиши примеры прямо пропорциональных величин. Запиши формулу прямой пропорциональности.

 

2. Определение пропорции. Пример пропорции. Крайние и средние члены

 

3. Что означает 10-6

Запишите с отрицательным показателем выражение 3\103

В3

1. Статистические характеристики. Пример ситуации, где вычисляется среднее арифметическое числового ряда

 

 

2. (в-с)/2а, найти значение выражения при в=-3, с=5, а=4


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.