ПРОИЗВОДНАЯ_1

ПРОИЗВОДНАЯ_1

y¢ = 3

Ответ. 6

На рисунке изображен график функции y = f(x), определенной на интервале (−8; 3). 1) Найдите количество точек, в которых производная функции f (x) равна 0. 2) Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 18.

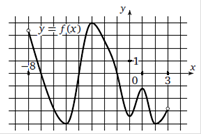Ответ. 5

На рисунке изображен график производной функции f(x), определенной на интервале (−8; 5). В какой точке отрезка [0;4] f(x) принимает наименьшее значение?

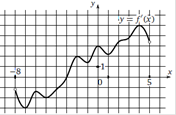1. Отметим отрезок [0;4] 2. Производная положительная – функция возрастает. 3. Наименьшее значение принимает в точке 0. Ответ. 0

На рисунке изображен график производной функции f(x), определенной на интервале (−10; 3). В какой точке отрезка [−4;−1] f(x) принимает наибольшее значение?

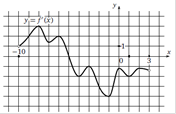1. Отметим отрезок [−4;−1] 2. Производная отрицательная – функция убывает. 3. Наибольшее значение принимает в точке -4. Ответ. -4

На рисунке изображен график производной функции f(x), определенной на интервале (−11;3). Найдите количество таких чисел x_i, что касательная к графику функции f(x) в точке с абсциссой x_i параллельна прямой y = 3x − 11 или совпадает с ней.

y¢ = 3

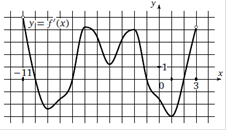
y = 3x – 11

На рисунке изображен график производной функции f(x), определенной на интервале (−5; 3). Найдите абсциссу точки, в которой касательная к графику функции f (x) параллельна прямой y = 2x+7 или совпадает с ней.

y’ = 2

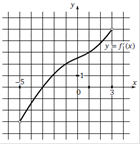
1. Найдем производную

y = 2x+7 y¢ = 2

2. Проведем прямую y¢ = 2

3. Найдем абсциссу (х) точки пересечения прямой с графиком производной

12 Следующая ⇒