Примеры решения задач по теме: Задачи на составление уравнений прямой на плоскости.

Примеры решения задач по теме: Задачи на составление уравнений прямой на плоскости.

1.Составить уравнение прямой, проходящей через т. М (1; 1) параллельно прямой у = 2х + 1.

Решение: Рассмотрим исходные данные задачи, используем уравнение прямой с угловым коэффициентом, проходящей через заданную точку:

у – у₀ = k(х – х₀).

В заданном уравнении k₁=2, учитывая условие параллельности прямых k₁= k₂, имеем, что k₂ = 2. Известно, что т. М (1; 1) принадлежит прямой, подставим координаты точки М в заданное уравнение, тогда искомое уравнение примет вид:

у – 1 = 2(х – 1);

у = 2х – 1.

Ответ: у = 2х – 1.

2. Составить уравнение прямой, проходящей через т. N (3; 1) перпендикулярно прямой у = – 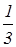х + 2.

Решение: Рассмотрим общий вид уравнения прямой с угловым коэффициентом и проходящей через заданную точку:

у – у₀ = k(х – х₀).

В заданном уравнении k₁= – 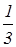, учитывая условие перпендикулярности прямых k₁= –1/ k_{2 ,}получаем, что k₂ = 3.

Так как точка N (3; 1) принадлежит прямой, подставим координаты точки в уравнение. Тогда уравнение примет вид:

у – 1 = 3 · (х – 3);

у = 3х – 8.

Ответ: у = 3х – 8.

3.Составить уравнение прямой, проходящей через т. А (5; 2) и отсекающей на осях системы координат равные отрезки.

Решение: Рассмотрим уравнение прямой в отрезках 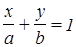, подставим координаты точки А в уравнение с учетом того, что прямая отсекает на осях одинаковые отрезки. Предположим, что длина отрезка равна а, тогда имеем 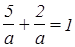, откуда получим,

что а = 7. Тогда уравнение прямой примет вид:

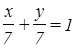, или х + у = 7

Ответ: х + у = 7.

12 Следующая ⇒