
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задачи, где применяется геометрическая интерпретация
№3) Задачи, где применяется геометрическая интерпретация
Тренировочная работа20, №17 (про фермера)
У фермера есть два поля, каждое площадью 10 га. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц/га, а на втором – 200 ц/га. Урожайность свёклы на первом поле составляет 200 ц/га, а на втором – 300 ц/га.
Фермер может продавать картофель по цене 10 000 р/ц, а свёклу – по цене 13 000 р/ц. Какой наибольший доход может получить фермер?
Решение (по Максютину).
| 1 поле | S | Урожай | Выручка |
| картофель | х га | 300 х ц | 10 000 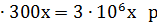
|
| свёкла | 10 – х га | 200(10 – х) ц | 13 000 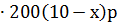 =
26 =
26 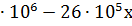 р р
|
| Всего | 26 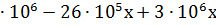 р р
|
| 2 поле | S | Урожай | Выручка |
| картофель | у га | 200 у ц | 10 000 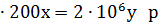
|
| свёкла | 10 – у га | 300(10 – у) ц | 13 000 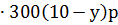 =
39 =
39 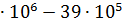 у р у р
|
| Всего | 39 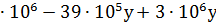 р р
|
Общий доход:
26 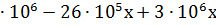 + 39
+ 39 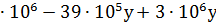 =
= 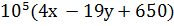 р
р
Обозначим 4х – 19у + 650 = с Выразим у через х и найдём значение с при котором у принимает наибольшее значение:
у = 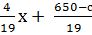 . Заметим х
. Заметим х 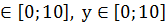 – это квадрат со стороной 10. Целевая функция у =
– это квадрат со стороной 10. Целевая функция у = 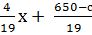 . – это множество прямых, параллельных прямой у =
. – это множество прямых, параллельных прямой у =  через точки указанного квадрата, а некоторые – нет. Рассмотрим две угловые «крайние» точки (0;10) и (10;0), подставляя координаты этих точек, найдём наибольшее значение
через точки указанного квадрата, а некоторые – нет. Рассмотрим две угловые «крайние» точки (0;10) и (10;0), подставляя координаты этих точек, найдём наибольшее значение
с = 690. 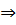 умножая на
умножая на 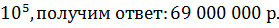
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|