Главная Контакты Случайная статья Автоматизация Антропология Археология Архитектура Биология Ботаника Бухгалтерия Военная наука Генетика География Геология Демография Деревообработка Журналистика Зоология Изобретательство Информатика Искусство История Кинематография Компьютеризация Косметика Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Материаловедение Медицина Менеджмент Металлургия Метрология Механика Музыка Науковедение Образование Охрана Труда Педагогика Полиграфия Политология Право Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Электротехника Энергетика
	Расстояние между параллельными плоскостями ⇐ ПредыдущаяСтр 2 из 3Следующая ⇒ Расстояние между параллельными плоскостями
Расстоянием между двумя параллельными плоскостями называется расстояние от произвольной точки одной плоскости до второй плоскости.	β || α, B ∈ β, ρ (β; α) = ρ (B; α). Выбираем в плоскости β произвольную точку B и находим расстояние от этой точки до плоскости α.
Расстояние между скрещивающимися прямыми
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них. Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Она равна расстоянию между параллельными плоскостями, которые проходят через эти прямые.	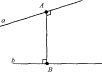	AB ⊥ a, AB ⊥ b; ρ (a; b) = AB. Прямые a и b — скрещивающиеся.

2)Решить задачи (по примерам):

1. Два отрезка длин, а и b упираются концами в две параллельные плоскости. Проекция первого отрезка (длины, а) на плоскость равна с. Найдите проекцию второго отрезка, если, а = 13, b = 15, с = 5 см.

2. Две параллельные плоскости расстояние между которыми 6 дм, пересечены прямой, составляющей с каждой из плоскости угол в 30⁰. Найти длину отрезка этой прямой, заключенной между плоскостями.

3. Расстояние между параллельными плоскостями равно 10 см. Отрезок прямой длина которого 26 см расположен между ними так, что его конец принадлежит плоскости. Найти проекцию этого отрезка на другую плоскость.

4. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ если: а) АС = 3 м, ВD = 4 м, СD = 12 м, б) АD = 4 м, ВС = 7 м, СD = 1 м.

5. Плоскости α и β перпендикулярны. В плоскости α взята точка А, расстояние от которой до прямой с (линия пересечения плоскостей ) равно 0,9 м. В плоскости β проведена прямая b, параллельная прямой с и отстоящая от нее на 1,2 м. Найдите расстояние от точки А до прямой b.