
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расстояние между прямой и параллельной ей плоскостью
ПЗ. Признаки и свойства параллельных и перпендикулярных плоскостей. Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве.
Задание:
1)Перепишите и заполните пропуски:

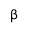 А)Пример 1. Два отрезка длин а и b упираются концами в две параллельные плоскости. Проекция первого отрезка (длины а) на плоскость равна с. Найдите проекцию второго отрезка, если а = 17 , b = 10, с = 15 см.
А)Пример 1. Два отрезка длин а и b упираются концами в две параллельные плоскости. Проекция первого отрезка (длины а) на плоскость равна с. Найдите проекцию второго отрезка, если а = 17 , b = 10, с = 15 см.


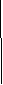 Дано:α || β, а = 17 , b = 10, с = 15 см. Найти:х
Дано:α || β, а = 17 , b = 10, с = 15 см. Найти:х
Решение:
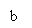
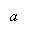
 а2 – с2 = b2 – х2, х2 = b2 – а2 + с2 , х2 = 102 – 172 + 152 =
а2 – с2 = b2 – х2, х2 = b2 – а2 + с2 , х2 = 102 – 172 + 152 =
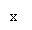
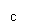

 = 100 – 289 + 225 = …, х = … см.
= 100 – 289 + 225 = …, х = … см.
Ответ: х = 6 см.
 Пример 2.
Пример 2.
Две параллельные плоскости расстояние между

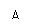
 которыми 2 дм, пересечены прямой, составляющей с каждой из
которыми 2 дм, пересечены прямой, составляющей с каждой из
плоскости угол в 300. Найти длину отрезка этой прямой, заключенной
 между плоскостями.
между плоскостями.
Дано: α || β, АВ∩α = А, АВ∩β = В, Ð АВС = 30°, АС = 2 дм.
Найти:АВ

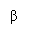
 Решение:Δ АСВ – прямоугольный, Ð АВС = 30°, АС = 2 дм.
Решение:Δ АСВ – прямоугольный, Ð АВС = 30°, АС = 2 дм.
 АВ = 2
АВ = 2  АС = 2
АС = 2  2 = … дм.
2 = … дм.
Ответ: АB = 4 дм.
Пример 3. Расстояние между параллельными плоскостями равно 8 см. Отрезок прямой длина которого 17 см расположен между ними так, что его конец принадлежит плоскости. Найти проекцию этого отрезка на другую плоскость.
Дано: α || β, АВ∩α = А, АВ∩β = В, АВ = 17 см, АС = 8 см.
Найти:ВС
Решение:Δ АСВ – прямоугольный, ВС2 = АВ2 – АС2 = 172 – 82 = 289 – 64 = …, ВС = … см.
Ответ: BС = 15 см.
Пример 4. На параллельных плоскостях α и β, выбрано по паре точек А1,А2 и В1,В2 соответственно так, что прямые А1В1 и А2В2 пересекаются в точке S Вычислите SА1 и SВ2, если А1В1= 6см; SА2 = 2,5см; SВ2 : SА2 = 3 : 1 . S
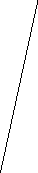
 Дано: α || β, А1 А2∩В1 В2 = S, А1, А2
Дано: α || β, А1 А2∩В1 В2 = S, А1, А2 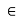 α, В1 ,В2
α, В1 ,В2 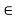 β,
β,
А1В1= 6см; SА2 = 2,5см; SВ2 : SА2 = 3 : 1
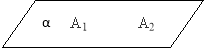 Найти:SА1, SВ2
Найти:SА1, SВ2
Решение:Δ SА1 А2 ~ Δ SВ1В2 , (α || β), SВ2 : SА2 = 3 : 1, SА2 = 2,5см,
 SВ2 = 3
SВ2 = 3 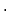 2,5 = … см. SВ1 : SА1 = 3 : 1, А1В1= 6см, SА1 = х ,
2,5 = … см. SВ1 : SА1 = 3 : 1, А1В1= 6см, SА1 = х ,
( х + 6 ) : х = 3 : 1, 3х = х + 6 , 2х = 6, х = …, SА1 = … см.

 Ответ: SА1 = 3 см, SВ2 = 7,5 см .
Ответ: SА1 = 3 см, SВ2 = 7,5 см .
В)Пример 1. Из точек А и В, лежащих в двух перпендикулярных
плоскостях, опущены перпендикуляры АС и ВD на прямую
пересечения плоскостей. Найдите длину отрезка АВ если:
 а) АС = 6 м, ВD = 7 м, СD = 6 м, б) АD = ВС = 5 м, СD = 1 м.
а) АС = 6 м, ВD = 7 м, СD = 6 м, б) АD = ВС = 5 м, СD = 1 м.
Решение:а)Пусть плоскости α и β перпендикулярны. СD – прямая пересечения плоскостей, тогда АС ⊥СВ и ВD ⊥ АD. Тогда в Δ АСВ:
АВ2 = АС2 + ВС2, но из Δ СDВ следует, что: ВС2 = СD2 + ВD2 , так что
АВ2 = АС2 + СD2 + ВD2. АВ2 = 62 + 72 + 62 = 36 + 49 + 36 = …, АВ = …
б) АВ2 = АС2 + ВС2, но из Δ СDА следует ,что: АС2 = АD2 – СD2 ,
 так что АВ2 = АD2 – СD2 + ВС2. АВ2 = 52 – 12 + 52 = 25 – 1 + 25 = …, АВ = … Ответ:а) 11 м, б) 7 м.
так что АВ2 = АD2 – СD2 + ВС2. АВ2 = 52 – 12 + 52 = 25 – 1 + 25 = …, АВ = … Ответ:а) 11 м, б) 7 м.
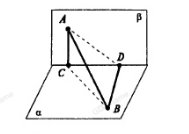
Пример 2.Плоскости α и β перпендикулярны. В плоскости α взята точка А, расстояние от которой до прямой с (линия пересечения плоскостей) равно 0,5 м. В плоскости β проведена прямая b, параллельная прямой с и отстоящая от нее на 1,2 м. Найдите расстояние от точки А до прямой b.
Решение:Пусть α ⊥ β , b || с, ВС = 1, АВ = 0,5м , где АВ ⊥с и ВС ⊥ b.
Тогда по теореме о 3 – х перпендикулярах АС ⊥ b. Так что
АС – искомое расстояние и АС2 = АВ2 + ВС2 = 1,22 + 0,52 = 1,44 + 0 ,25 = …, АС = …
Ответ: АС = 1,3 м.
С) Построить таблицу:
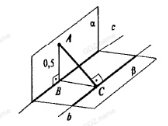
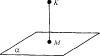
| Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость. | ||
Проводим KM ⊥ α
(M ∈ α). KM = ρ (K; α).
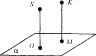
| SO ⊥ α.
Проводим KM || SO.
Тогда KM ⊥ αи KM = ρ (K; α).
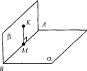
| Проводим через точку K плоскость β ⊥ α (β пересекает α по AB). Проводим KM ⊥ AB.
Тогда KM ⊥ α и KM = ρ (K; α).
|
Расстояние между прямой и параллельной ей плоскостью
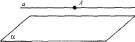
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|