Аналитические методы

Аналитические методы

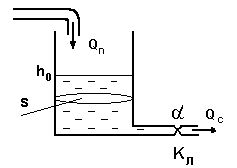
В качестве примера рассмотрим аналитическую процедуру получения передаточной функции бака с жидкостью (Рис.1). В баке будет осуществляться стабилизация уровня жидкости на номинальном значении 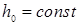. Регулирование притока 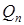осуществляется через верхнюю трубу.

Слив жидкостиидет через нижнюю трубу с установленном на ней

Рис.1 Объект управления – бак с жидкостью

клапане 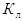. Степень открытия клапана a может изменяться от 0 до 1, устанавливая тем самым нужную величину стока. Площадь сечения бака 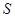. Очевидно, что в установившемся режиме работы приток равен стоку .

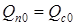Таким образом, управляющей величиной является приток жидкости, управляемой - величина уровня, а главным возмущением - изменение величины степени открытия 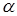клапана.

Пусть приток жидкости в бак увеличился на 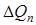. В это случае текущее значение притока будет равно 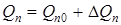. Тогда за время уровень возрастет на величину и составит 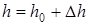. Очевидно, что количество жидкости накопленной во времени должно равняться количеству жидкости накопленной в объеме. Отсюда следует уравнение материального баланса

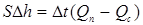Для анализа изменения уровня преобразуем это уравнение к виду

(1.1)

Из физики известно, что величина стока связана с уровнем соотношением

. (1.2)

Эта зависимость носит нелинейный характер. Для получения линейного дифференциального уравнения объекта и его передаточной функции необходимо произвести линеаризацию нелинейности в окрестности рабочей точки регулирования. Такой подход справедлив, т.к. при использовании регулятора стабилизации, отклонения текущего значения уровня от заданного будут малыми.

Для линеаризации необходимо разложить функцию (1.2) в ряд Тейлора и отбросить все нелинейные члены. Проделав это, получим

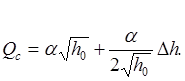С учетом этой зависимости уравнение (1.1) примет вид

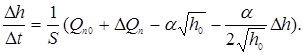Беря предел, при 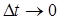, произведя замену переменных 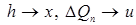, и учитывая, что 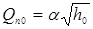получим дифференциальное уравнение объекта

. (1.3)

Известно, что инерционное звено первого порядка с коэффициентом усиления 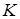и постоянной времени 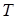описывается дифференциальным уравнением

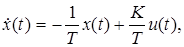(1.4)

Тогда, из сравнения формул (1.3) и (1.4) получим следующие выражения для постоянной времени и коэффициента усиления бака с жидкостью

Достоинства аналитических методов:

- не требуют проведения экспериментов на реальном объекте;

- позволяют определить математическое описание еще на стадии проектирования системы управления;

- позволяют учесть все основные особенности динамики объекта управления, как-то наличие нелинейностей, нестационарность, распределенные параметры и т.д.;

- обеспечивают получение универсального математического описания, пригодного для широкого класса аналогичных объектов управления.

Недостатки:

- трудность получения достаточно точной математической модели, учитывающей все особенности реального объекта;

- проверка адекватности модели и реального процесса требуют проведения натурных экспериментов;

- многие математические модели имеют ряд трудно оцениваемых в численном выражении параметров (например, константы скоростей химических реакций).

⇐ Предыдущая 12