
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Синус, косинус и тангенс суммы и разности двух углов.
Урок
Задание: изучить материал урока по конспекту, учебнику Алимова Ш.А. «Алгебра и начала математического анализа. 10-11 классы. Базовый и углубленный уровни. Учебник. ФГОС» §28 и видеофрагменту; выполнить самостоятельную работу и ответить письменно на контрольные вопросы.
Тема: Синус, косинус и тангенс суммы и разности двух углов.
Цель: научиться применять формулы сложения в различных заданиях.
Ход урока
1. Объяснение нового материала.
На практике часто приходиться двухфазный или трехфазный ток направлять в один проводник. При этом возникает, как показал опыт, "суммарный" переменный ток, мгновенная сила которого равна сумме мгновенных сил слагаемых токов. Точную величину амплитуды "суммарного" тока, его частоту и фазу смещения не найти, не рассмотрев предварительно свойства тригонометрических функций, связанных со сложением аргументов.
Сегодня мы рассмотрим так называемые формулы сложения: «Синус, косинус и тангенс суммы и разности двух углов».
Эго следующие формулы:
cos ( ) = cos cos - sin sin ; (1)
cos ( - ) = cos cos + sin sin ; (2)
sin ( + ) = sin cos + sin cos ; (3)
sin ( - ) = sin cos - sin cos ; (4)
| b |
| В |
| С |
| D |
| α |
| β |
| А |
| h |
| c |
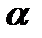 +
+ 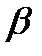 ) =
) = 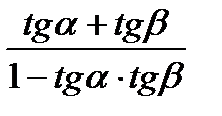 ;(5)
;(5)
tg ( - ) = . (6)
Рассмотрим доказательство формулы (1)
Для этого рассмотрим треугольник АВС, в котором проведём высоту АD, которая разобьёт угол А на сумму двух углов 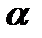 +
+ 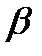 ,и вспомним формулы площадей треугольников.
,и вспомним формулы площадей треугольников.
| S∆ADB = ½ c h sinα S∆ADC = ½b h sinβ S∆ABC=S∆ADC+S∆ADB, гдеS∆ABС = ½bс sin (α+β) ½bс sin (α+β) = ½ c h sinα + ½b h sinβ bс sin (α+β)= c h sinα + b h sinβ Разделим на bс sin (α+β)= h/b sinα + h/с sinβ sin (α+β)= cosβ sinα + cosα sinβ |
Формула доказана.
Рассмотрим несколько примеров на применение этих формул.
1.Вычислите: а) sin 75o; б) sin 150;
а) sin 75o = sin (45o + 30o) = sin 45o · cos30o + cos 45o ·sin 30o = 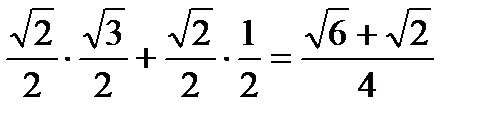
б) sin 150 = sin(450 – 300) = sin450 ∙ cos300 – cos450 ∙ sin 300
2. Доказать, что:
sin ( 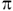 + х) = – sinx
+ х) = – sinx
cos ( 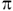 + х) = – cosx
+ х) = – cosx
Решение:
sin ( 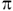 + х) = sin
+ х) = sin 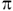 ·cosx + cos
·cosx + cos 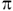 ·sinx = 0 ·cosx + (– 1) ·sinx = – sinx
·sinx = 0 ·cosx + (– 1) ·sinx = – sinx
cos ( 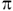 + х) = cos
+ х) = cos 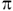 ·cosx + sin
·cosx + sin 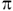 ·sinx = (– 1)·cosx – 0 ·sinx = – cosx
·sinx = (– 1)·cosx – 0 ·sinx = – cosx
3.Вычислите: sin (x + y), если известно, что
sin x = 3/5, 0 < x < 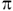 /2 ; cos y = – 3/5,
/2 ; cos y = – 3/5, 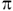 < y < 3
< y < 3 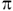 /2
/2
Решение:
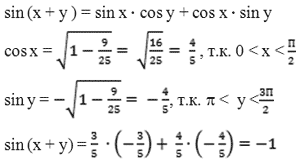
Oтвет: –1
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|