
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Закрепление учебного материала
Закрепление учебного материала
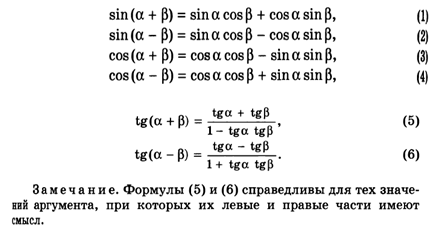 |
1.Синус суммы двух углов можно получить следующим образом:
- вычисляем произведение синуса первого угла на косинус второго;
- умножаем косинус первого угла на синус первого;
- складываем получившиеся значения.
Графическое написание формулы выглядит так: sin (α+β)=sin α⋅cos β+cos α⋅sin β
2. Синус разности вычисляется почти так же, только полученные произведения нужно не сложить, а вычесть друг из друга. Таким образом, вычисляем произведения синуса первого угла на косинус второго и косинуса первого угла на синус второго и находим их разность. Формула пишется так: sin (α−β)=sin αcos β+sin αsin β
3. Косинус суммы. Для него находим произведения косинуса первого угла на косинус второго и синуса первого угла на синус второго соответственно и находим их разность: cos (α+β)=cos αcos β−sin αsin β
4. Косинус разности: вычисляем произведения синусов и косинусов данных углов, как и ранее, и складываем их. Формула: cos (α−β)=cos α⋅cos β+sin α⋅sin βcos (α-β)=cos α·cos β+sin α·sin β
5. Тангенс суммы. Эта формула выражается дробью, в числителе которой – сумма тангенсов искомых углов, а в знаменателе – единица, из которой вычитается произведение тангенсов искомых углов. Все понятно из ее графической записи: tg (α+β)=tg α+tg β1−tg α⋅tg βtg (α+β)=tg α+tg β1-tg α·tg β
6. Тангенс разности. Вычисляем значения разности и произведения тангенсов данных углов и поступаем с ними схожим образом. В знаменателе мы прибавляем к единице, а не наоборот: tg (α−β)=tg α−tg β1+tg α⋅tg βtg (α-β)=tg α-tg β1+tg α·tg β
7. Котангенс суммы. Для вычислений по этой формуле нам понадобятся произведение и сумма котангенсов данных углов, с которыми мы поступаем следующим образом: ctg (α+β)=−1+ctg α⋅ctg βctg α+ctg βctg (α+β)=-1+ctg α·ctg βctg α+ctg β
8. Котангенс разности. Формула схожа с предыдущей, но в числителе и знаменателе – минус, а не плюс ctg (α−β)=−1−ctg α⋅ctg βctg α−ctg βctg (α-β)=-1-ctg α·ctg βctg α-ctg β.
Вы, наверное, заметили, что эти формулы попарно схожи. При помощи знаков ±(плюс-минус) и ∓(минус-плюс) мы можем сгруппировать их для удобства записи.
Теперь мы докажем следующую формулу – косинуса суммы. Это проще, поскольку мы можем воспользоваться предыдущими расчетами. Возьмем представление α+β=α−(−β)α+β=α-(-β). У нас есть:
cos (α+β)=cos (α−(− β))==cos α⋅cos (−β)+sin α⋅sin (−β)==cos α⋅cos β+sin α⋅sin β cos (α+β)=cos (α-(- β))==cos α·cos (-β)+sin α·sin (-β)==cos α·cos β+sin α·sin β
Это и есть доказательство формулы косинуса суммы. В последней строчке использовано свойство синуса и косинуса противоположных углов.


Пример 4

Пример 5

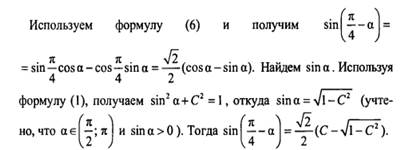
Пример 6

Пример 7

Пример 8

Пример 9

Самостоятельная работа.



Контроль знаний
Ответы на выполненное задание (в файлах может быть текст, скриншоты, фотографии, таблицы и т.д.) высылайте на электронный ящик преподавателя:
kacha_s_s@mail.ru
Литература
1. https://zaochnik.com/spravochnik/matematika/trigonometrija/formuly-slozhenija-dokazatelstvo-primery/
2. https://resh.edu.ru/subject/lesson/4734/conspect/199304/https://www.yaklass.ru/materiali?mode=lsntheme&themeid=13
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|