
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Рассмотрим действия над числами
Рассмотрим действия над числами
Сложение
Z 1 + Z 2 = (a 1 + b 1 i) + (a 2 + b 2 i) = a 1 + b 1 i + a 2 + b 2 i = (a 1 + a 2) + (b 1 + b 2) i
Вычитание
Z 1 - Z 2 = (a 1 + b 1 i) - (a 2 + b 2 i) = a 1 + b 1 i - a 2 - b 2 i = (a 1 - a 2) + (b 1 - b 2) i
Умножение
Z 1  Z 2 = (a 1 + b 1 i)
Z 2 = (a 1 + b 1 i)  (a 2 + b 2 i) = a 1
(a 2 + b 2 i) = a 1  a 2 + b 1
a 2 + b 1  а 2 i + a 1
а 2 i + a 1  b 2 i + b 1
b 2 i + b 1  b 2 i 2 =
b 2 i 2 =
= a 1  a 2 + i (b 1
a 2 + i (b 1  а 2 + a 1
а 2 + a 1  b 2) - b 1
b 2) - b 1  b 2 = (a 1
b 2 = (a 1  a 2 - b 1
a 2 - b 1  b 2) + (b 1
b 2) + (b 1  а 2 + a 1
а 2 + a 1  b 2) i
b 2) i
Например
1) (3 - 5 i)  (- 3 + i) = - 9 + 15 i + 3 i - 5 i 2 = - 9 +18 i + 5 = - 4 + 18i;
(- 3 + i) = - 9 + 15 i + 3 i - 5 i 2 = - 9 +18 i + 5 = - 4 + 18i;
т.к. i 2 = - 1, то -5  (-1) = 5
(-1) = 5
2) (2 - 3 i)  (2 + 3 i) = 4 - 9 i 2 = 4 + 9 = 13
(2 + 3 i) = 4 - 9 i 2 = 4 + 9 = 13
( a + b i )  ( a - b i ) = a 2 - b 2 i 2 = a 2 + b 2
( a - b i ) = a 2 - b 2 i 2 = a 2 + b 2

Сумма квадратов
Сумма квадратов разлагается на множители только во множестве комплексных чисел
Деление
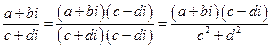
конкретно на примере:
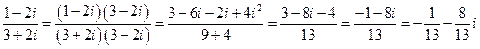
Возведение в квадрат, куб (используем формулы сокращенного умножения)
Z = ( a + b i ) 2 = a 2 + 2 a b i + b 2 i 2 = a 2 + 2 a b i - b 2;
например:
1) ( - 4 + i ) 2 = 16 - 8 i + i 2 = 16 - 8 i - 1 = 15 - 8 i
2) ( 2 - 3 i ) 3 = 8 - 3  22
22  3 i + 3
3 i + 3  2
2  ( - 3 i ) 2 - 27 i 3 = 8 - 36 i + 54 i 2 - 27 i 3 =
( - 3 i ) 2 - 27 i 3 = 8 - 36 i + 54 i 2 - 27 i 3 =
= 8 - 36 i - 54 + 27 i = - 46 - 9 i
Выполнить действия
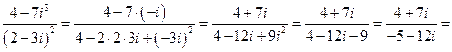
при этих действиях использованы правила: i3=-i; i2=-1; (a-b)2=a2-2∙a∙b+b2, а теперь разделим, для этого умножим знаменатель на сопряженное ему число (-5 + 12i) , а чтобы дробь не изменилась, умножаем и числитель на это число, т.е.
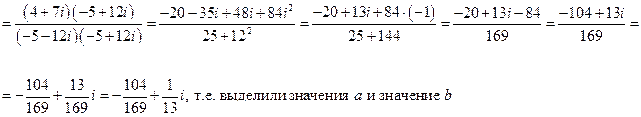
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|