КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ

Стр 1 из 2Следующая ⇒

КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ

х² + 4 = 0 х² = - 4 во множестве R решений нет

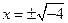
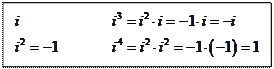
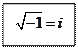Обозначим:

Множество действительных чисел и мнимая единица составляют множество комплексных чисел, тогда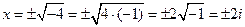

i ²³ = i ³ = - i (23 : 4 = 4 5 + 3)

i ²³ = i ²⁰ i ³ = 1 (-i) = - i i ⁴⁸ = i⁰ = 1 i ¹⁰ i ⁸ i ² = 1 (-1) = -1 i ¹⁴ = i ² = - 1

i ²⁵ = i ¹ = i i ¹⁰³ = i³ = - i 2 i³ - 7 i ⁸ + 5 i ⁹ + 4 i¹⁰ = - 2 i - 7 + 5 i - 4 = - 11 + 3 i

Число Z = a + b i - комплексное число (алгебраическая форма записи)

а - действительная часть числа

b i - мнимая часть числа

a + b i = a₁ + b₁ i если а = а₁ b = b₁

a + b i и a - b i называются сопряженными

Например

2 - 3 i и 2 + 3 i

- 4 - i и - 4 + i , т. е. отличаются знаком перед мнимой частью

Числа a + b i и - a - b i называются противоположными

Например

- 3 - 4 i и 3 + 4 i

- 5 + 2 i и 5 - 2 i , т.е. отличаются знаками и перед мнимой и перед действительной частями

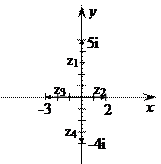
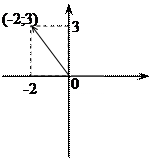
Комплексные числа изображаются геометрически точкой (a; b) или радиусом - вектором, проведенным к этой точке из начала координат

Z ₁ = 5i Z ₂ = 2 Z ₃ = - 3i Z ₄ = - 4i

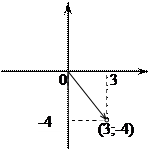
Z = 3 - 4 i Z = - 2 + 3 i

Изобразите числа:

Z = - 7 + 2 i Z = - 9 - i

Z = - 1 - 4 i Z = 12

Z = - 5 i Z = 6 i

Z = - 4 Z = - 3 - 2 i

Итак: a + bi, a 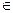OX I ч j > 0 острый,

b OY II ч j > 0 тупой j = 180 ⁰ - j₁

III ч j < 0; тупой j = - (180 ⁰ - j₁)

IV ч j < 0; острый

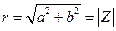– модуль комплексного числа

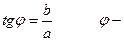аргумент комплексного числа

Найти модуль и аргумент комплексного числа:

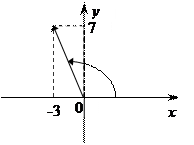
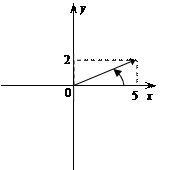а) Z = 5 + 2 i

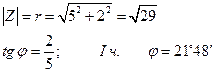
б) Z = - 3 + 7 i

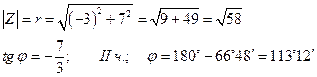
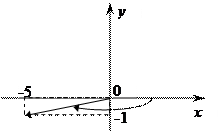
в) Z = - 5 - i

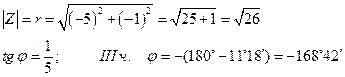
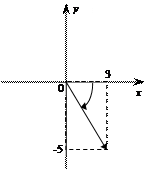
г) Z = 3 - 5 i

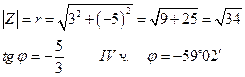
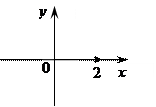Для чисел, состоящих только из мнимой или только действительной частей нахождение 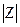и 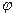упрощается:

1) Z = 2

2 = 2 + 0i Число находится на "ОХ"

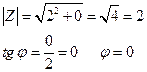
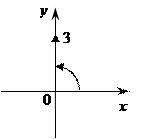
2) Z = 3i

3i = 0 + 3i Число находится на "ОУ"

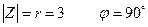
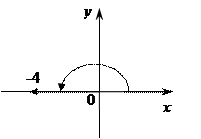
3) Z = - 4

Число находится на "ОХ" (влево)

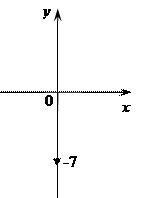4) Z = - 7 i

Число находится на "ОУ" (вниз)

Z₁ = a ₁ + b ₁ i

Пусть даны числа: Z₂ = a ₂ + b ₂ i

12 Следующая ⇒