Нелинейная часть.. Определим передаточную функцию системы.

2. Нелинейная часть.

Структурная схема с нелинейным элементом имеет вид:

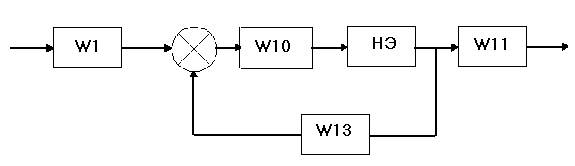
Здесь,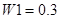

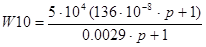
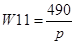
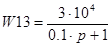
Нелинейный элемент имеет статическую характеристику вида:

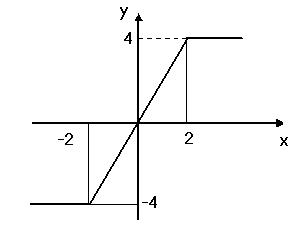
С точки зрения энергетических затрат, использование нелинейных элементов нецелесообразно. Проанализируем статическую характеристику данного нелинейного элемента на трех ее участках.

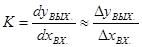- передаточная функция звена.

Тогда на первом и третьем участках 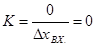, то есть на них система не работоспособна.

Работает система только на втором участке, где 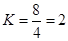или по-другому можно записать: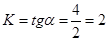

Таким образом, нелинейный элемент в данной схеме целесообразней заменить линейным элементом с передаточной функцией W15=K, где К=2 – коэффициент усиления.

Эквивалентная линеаризованная структурная схема примет вид:

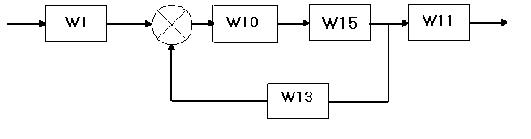
2.1 Определим передаточную функцию системы.

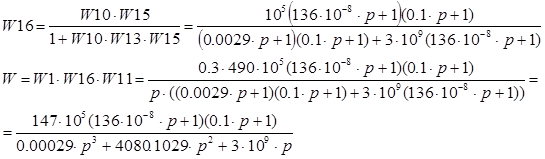
Определим устойчивость системы с помощью критерия Гурвица. Характеристическое уравнение найденной передаточной функции имеет вид:

0.00029p³+4080.1029p²+3 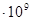p=0

Используя данное уравнение составим главный определитель Гурвица.

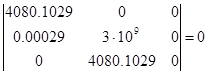
Из главного определителя выделим диагональные миноры:

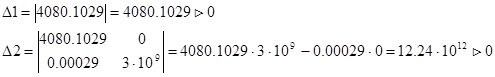
То есть, система опять находится на границе устойчивости, так как главный определитель Гурвица равен нулю.

Проверим устойчивость системы по критерию Ляпунова. Для этого найдем корни характеристического полинома полученной передаточной функции.

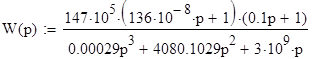
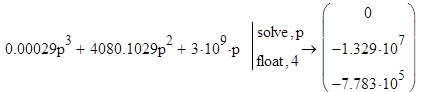
Так как в результате получили два отрицательных корня и один нулевой, то, согласно критерию Ляпунова, можно сделать вывод, что система находится на границе устойчивости.

Передаточную функцию можно записать следующим образом:

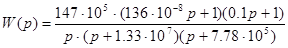или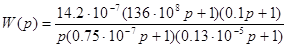

Если сравнить передаточную функцию, полученную в линейной части курсовой работы 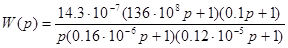с передаточной функцией линеаризованной системы 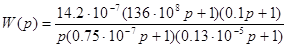, то можно сделать вывод, что их отличие мало. Следовательно, все характеристики также должны совпадать.

12 Следующая ⇒