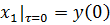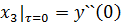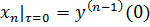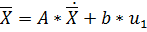- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Управляемость и наблюдаемость
МОДЕЛИ СИСТЕМ В ФОРМЕ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
Математическая модель системы в форме дифференциальных уравнений может быть задана различными способами:
· Дифференциальное уравнение n – го порядка;
· Система дифференциальных уравнений 1 – го порядка (n – уравнений);
· Модель в форме пространства состояний
МОДЕЛЬ В ПРОСТРАНСТВЕ СОСТОЯНИЙ
1.1 Переход от ОДУ n –го порядка к модели в форме пространства состояний. («вх-вых»  «пр-во сост.»)
«пр-во сост.»)
Состояние одномерного объекта определяется не только измеряемой выходной переменной, но и скоростью ее изменения, ускорением и т.д. Эти величины: y, y`,y``,…,y(n) и относим к переменным состояния. В этом случае, ОДУ удобно представить в форме системы уравнений первого порядка (форма Коши).
Общий вид ММ в пространстве состояний:



y - выходная переменная;
u – управляющее воздействие.
A 
B 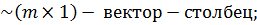
C 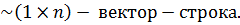
Переход от ОДУ n – го порядка к модели в пространстве состояний может быть осуществлен различными способами.
u x1 






|
|
xn
Модель вход – выход:
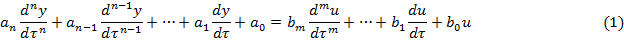
От описания в форме вход – выход необходимо перейти к описанию объекта в пространстве состояний. За переменную состояния примем не только y, но и y`, y``,…, y(n).
Запишем модель (1) в виде:
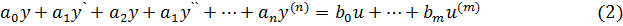
|
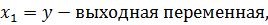
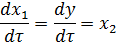
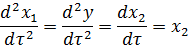
………………………….
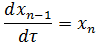
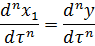
Из (2) имеем:
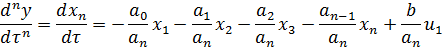
Таким образом, имеем систему уравнений:

В матричной форме (в развернутом виде):

 |
|
Данная форма называется «наблюдаемая» форма модели в пространстве состояний. 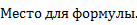
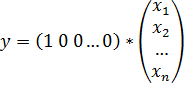
В Этом случае измеряется выходная переменная y.
|
Существуют и другие формы моделей в пространстве состояний, например
«управляемая» форма представления модели.
Представим ДУ (1) в операторной форме:

Обозначим:
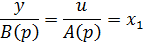
Выразим y и u через 

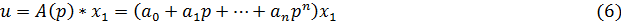
 Введем переменные состояния:
Введем переменные состояния:

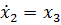 (7)
(7)

Воспользуемся (6), применим оператор P к 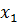 с учетом (7):
с учетом (7):
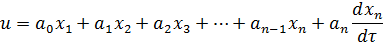
Определим:

Из (5) определим:

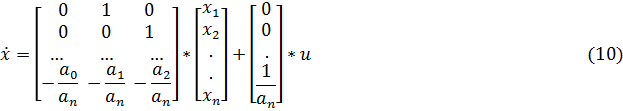
1.2 Переход от модели в пространстве состояний к модели «вход – выход».
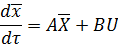
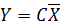
Преобразуем по Лапласу:
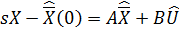 (*)
(*) 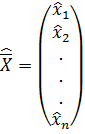
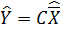
При нулевых начальных условиях 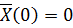 будем иметь:
будем иметь:


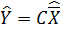
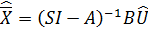
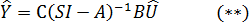
Отсюда передаточная функция объекта:
|
Из уравнения (*) с учетом начальных условий:
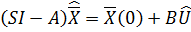
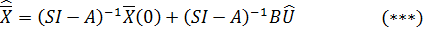
Оригинал вычисляется с помощью обратного преобразования Лапласа.
Для одномерного случая:
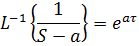
Для матричного варианта:


Второе слагаемое в (***) – произведение изображений, которому соответствует свертка оригиналов.
Таким образом, имеем оригинал:
|
Весовая функция объекта – реакция на единичный импульс: из (**) имеем:
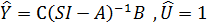
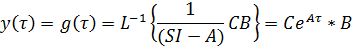
Переходная функция – это интеграл от функции веса.
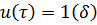
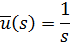
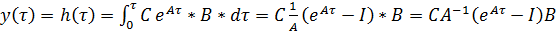 .
.
2. Управляемость и наблюдаемость
Модель системы:

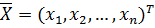
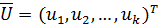
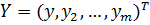

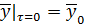
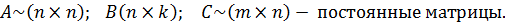
Система (объект) полностью управляем, если, с помощью 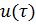 за конечное время
за конечное время 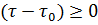 она может быть переведена из любого начального состояния
она может быть переведена из любого начального состояния 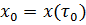 в любое наперед заданное состояние
в любое наперед заданное состояние 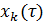 .
.
 Формально – математическое условие управляемости заключается в том, что ранг матрицы управляемости
Формально – математическое условие управляемости заключается в том, что ранг матрицы управляемости  равен n, т.е. матрица
равен n, т.е. матрица 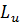 имеет полный ранг:
имеет полный ранг:
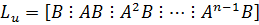
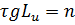 (2)
(2)
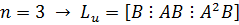
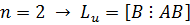
(имеется процедура в MATLABе)
Докажем условие (2)
u x 

|
|
 |
…. сист. (1):

Разложим в ряд:
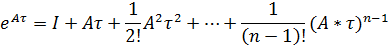
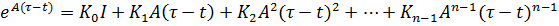
Подставим это выражение в (3):
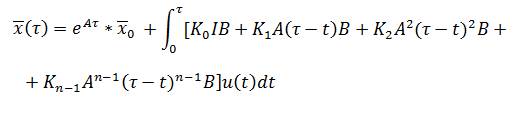
Данное выражение можно записать в матрично – векторной форме:
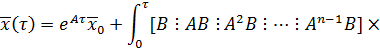
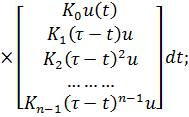
Управляющее воздействие u будет влиять на все состояния 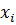 только тогда, когда строки матрицы
только тогда, когда строки матрицы 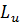 линейно независимы, т.е.
линейно независимы, т.е. 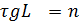 . В этом случае не будет нулевых строк в матрице
. В этом случае не будет нулевых строк в матрице 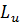 .
.
Условие управляемости по выходам можно получить умножив обе части (3) слева на матрицу С.
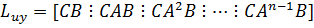

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|