
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
N итерации. Xi Базисные Переменные. Значения. Переменные Xj
Табл.1
N итерации
Xi Базисные Переменные
Значения
Переменные Xj
X3
X4
-1
-f
-1
X1
2 2/9
1
- 1/9
0
1/9
X3
22 7/9
0
1 1/9
1
- 1/9
-f
-22 2/9
0
1/9
0
-1 1/9
X1
4 1/2
1
0
1/10
1/10
X2
20 1/2
0
1
9/10
- 1/10
-f
-24 1/2
0
0
- 1/10
-1 1/10
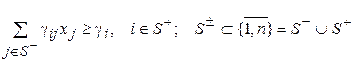 (8)
(8)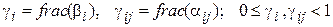
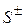 , соответственно;
, соответственно; 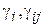 - дробные части коэффициентов
- дробные части коэффициентов 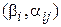 i-ого уравнения ограничений для Xi базисной переменной из таблицы1, выписанныеиз последней ее итерации -2.
i-ого уравнения ограничений для Xi базисной переменной из таблицы1, выписанныеиз последней ее итерации -2.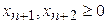 , получим уравнение отсекающей плоскости
, получим уравнение отсекающей плоскости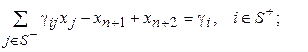 (9)
(9)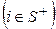 из последней таблицы1, для которой выполняется условие
из последней таблицы1, для которой выполняется условие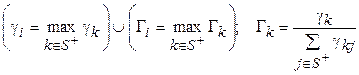 (10)
(10)