МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Стр 1 из 3Следующая ⇒

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Программное обеспечение вычислительной техники

и автоматизированных систем»

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

И КОНТРОЛЬНЫЕ ЗАДАНИЯ

Задачи целочисленного программирования

Ростов-на-Дону

Составитель: Золотарев А.А., Золотарева Л.И.

УДК 512.3

Методические указания и контрольные задания по курсам «вычислительная математика» и «методы оптимизации»

ДГТУ, г.Ростов-на-Дону, 2004, - 10с.

Методическая разработка предназначена для подготовки по специальностям 220400, 351500 в плане дисциплин: «методы оптимизации» и «теория принятия решений». Она содержит индивидуальные задания, характерные примеры и краткие пояснения, необходимые для успешного выполнения лабораторных работ и освоения изучаемой темы. Для проверки результатов наряду с обязательной частью по самостоятельной реализации алгоритмов контрольных заданий предполагается использование программных средств: надстройки «Поиск решения» табличного процессора MS Excel, либо специализированного пакета Simplex математического процессора Maple V.

Печатается по решению методической комиссии факультета автоматизации и информатики

Рецензенты: кандидат физико-математических наук

Е.Н. Румянцев.

ÓИздательский центр ДГУ, 2004

ВВЕДЕНИЕ

В работе рассматривается один из важнейших классов задач оптимизации – задачи целочисленного программирования. Обсуждаются особенности методов корректного их решения, рассматриваются характерные примеры реализации этих методов и приводятся варианты индивидуальных заданий для закрепления теоретического материала. Для проверки достоверности оптимального решения, полученного предлагаемыми аналитическими методами, иллюстрируется методика использования программных средств - надстройки «Поиск решения» табличного процессора MS Excel либо специализированного пакета Simplex математического процессора Maple V.

Многие прикладные проблемы (техники, экономики, менеджмента и др.) характерны тем, что в силу объективных свойств управляемые в них ресурсы (все или частично) могут принимать только целочисленные значения. Например, таким естественным требованиям целочисленности отвечают трудовые ресурсы, неделимые штучные изделия (автомобили, самолеты, компьютеры…), партии товаров и др.

Указанные проблемы могут быть сведены к задачам целочисленного программирования, являющимся частным случаем задач математического программирования. В линейной постановке они отличаются от задач линейного программирования лишь наличием дополнительных требований целочисленности, заключающихся в том, что переменные 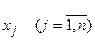соответствующей математической модели могут принимать только дискретные неотрицательные значения, т.е. значения из множества натуральных чисел N, дополненного нулем, т.е.

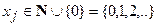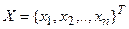, . (1)

Кажется на первый взгляд, что вполне естественным для решения такой полностью целочисленной задачи(ПЦЗ) является метод округления, когда на первом этапе решается задача линейного программирования без учета условий целочисленности (задача с ослабленными ограничениями - ЗОО), а на последующем этапе это полученное оптимальное решение округляется до целых значений. В действительности, как это будет показано ниже при разборе характерного примера, подход округления может дать допустимое целочисленное решение заметно отличающиеся от оптимального значения. Кроме того, указанный упрощенный метод решения ПЦЗ вовсе не применим, когда переменные модели могут принимать лишь значения из множества {0, 1}, что характерно для достаточно широкого подкласса ПЦЗ, называемых задачами булева программирования.

Известно, что линейная задача дискретного программирования может быть представлена в стандартной форме

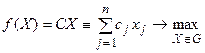(2)

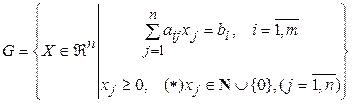(3)

где коэффициенты 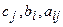известны. Тогда соответствующая задача с ослабленными ограничениями (ЗОО), являющаяся задачей линейного программирования, совпадает с полностью целочисленной задачей (ПЦЗ) (2),(3), за исключением ограничений целочисленности 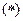, которые следует исключить из рассмотрения.

МЕТОД ОКРУГЛЕНИЙ

В стандартном виде (2),(3) рассмотрим, например, следующую ПЦЗ:

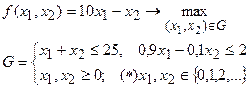(4)

Элементарными преобразованиями приведем ограничения G типа неравенства в (4) к условиям типа равенства. Тогда ПЦЗ в стандартной форме принимает вид

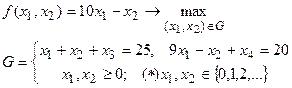(5)

Графическим методом (Рис.1) устанавливаем оптимальное решение соответствующей ЗОО

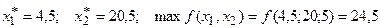. (6)

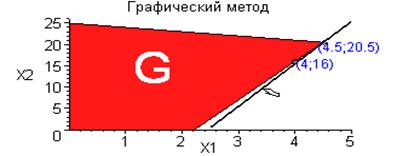Рис.1

Округление этого решения ЗОО до целочисленных значений дает лишь допустимое решение для ПЦЗ из области G

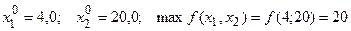
В действительности же оптимальное решение исходной ПЦЗ (4) имеет значение

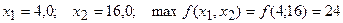, (7)

что заметно отличается от предыдущих решений как по значениям переменных модели, так и целевой функции.

МЕТОД ГОМОРИ (Отсекающих плоскостей)

Рассмотрим особенности реализации этого метода для решения ПЦЗ (2),(3) на характерном примере (4).

Вначале задачу (4) приводим к форме с целочисленными коэффициентами, затем – к стандартной форме (5). Решаем соответствующую (5) «ослабленную» задачу, без учета ограничений 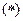. Применим для этого симплекс-метод[1,3], начальная таблица которого (на 0-ом шаге итераций) имеет вид:

12 3 Следующая ⇒