
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Иррациональные неравенства. Перечень вопросов, рассматриваемых в теме. Глоссарий по теме. Теоретический материал для самостоятельного изучения. Определение. Неравенство, содержащее переменную под знаком корня, называется иррациональным.
08.11.2021
1. Разобрать конспект лекции.
2. Формулы 1-3 и примеры 1-3 переписать в тетрадь.
Иррациональные неравенства
Цель:
получить знания об иррациональных неравенствах.
Задачи:
рассмотреть определения иррациональных неравенств;
познакомиться с основными видами иррациональных неравенств;
разобрать основные правила решения иррациональных неравенств.
Перечень вопросов, рассматриваемых в теме
1) понятие иррационального неравенства;
2) виды и методы решения простейших иррациональных неравенств.
Глоссарий по теме
Иррациональное неравенство– это неравенство, содержащее переменную под знаком корня.
Учебник:
1. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 – 11 классы: учебник для общеобразовательных организаций: базовый и углубленный уровни / Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др. – 3-е изд. – М.: Просвещение, 2016. – 463 с. §10.
Теоретический материал для самостоятельного изучения
Определение. Неравенство, содержащее переменную под знаком корня, называется иррациональным.
Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень: если в неравенство входит квадратный корень, то в квадрат; входит корень третьей степени − в куб и т.д.
Однако, возводить в квадрат, не нарушая равносильности, можно только неравенство, у которого обе части неотрицательны.
Иррациональное неравенство, как правило, сводится к равносильной системе (или совокупности систем) неравенств.
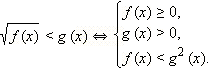 (1)
(1)
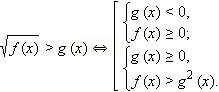 (2)
(2)
 (3)
(3)
1. Неравенства вида
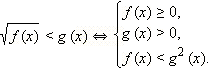
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|