
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
объемов тел.
объемов тел.
Фигура, ограниченная на плоскости ОХУ отрезком  оси ОХ, прямыми х=a, x=b и
оси ОХ, прямыми х=a, x=b и
графиком непрерывной и неотрицательной функции у = f(x) на [a,b], называется
криволинейной трапецией.
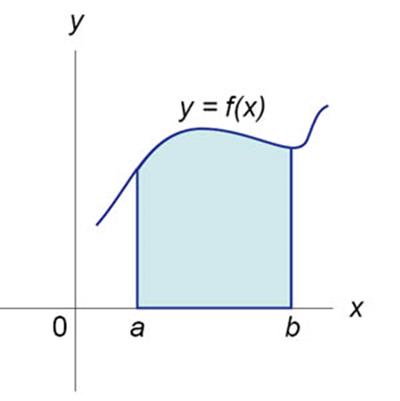
Площадь криволинейной трапеции вычисляется с помощью определенного интеграла:
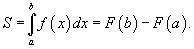
Пусть F (x) и G (x) - первообразные функций f (x) и g (x), соответственно.
Если f (x) ≥ g (x) на замкнутом интервале [a, b],
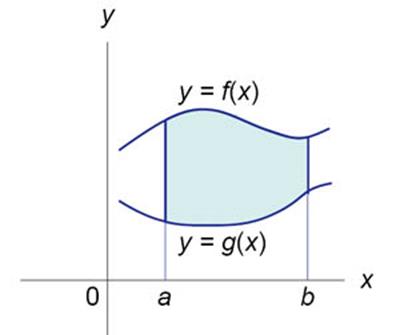
то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными
линиями x = a, x = b (рисунок 2), определяется формулой
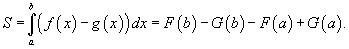
Вычисление объемов тел вращения:
Пусть дана кривая у=f(x), a≤x≤b. Объем тела вращения, ограниченного плоскостями х= a и х=b и поверхностью вращения кривой вокруг оси ОХ вычисляется по формуле:
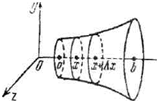
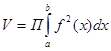
Аналогично можно получить формулу объема тела вращения вокруг оси ОУ
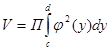 ;
;
Длина дуги кривой вычисляется по формуле:
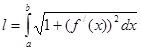
Если площадь сечения тела плоскостью, перпендикулярной оси Ох, выражена как функция
от х, т.е. в виде Ѕ = Ѕ(х) (а 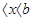 ), то объем части тела, заключенный между перпендикулярными
), то объем части тела, заключенный между перпендикулярными
оси Ох плоскостями х=а и х=b находится по формуле
V= 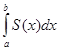
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|