
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Интегрирование по частям для определенного интеграла
Дата:19 ноября 2021г. группа:2-СПХ-5-20
Предмет:Прикладная математика.
Преподаватель:Шкурко Лариса Александровна
Тема занятия:3-я пара:«Геометрический смысл определенного интеграла. Свойства. Методы вычисления.».
Тип занятия– лекция по новой теме
Цели лекционного занятия:
1. Образовательная: Сформировать представления об интегральном исчислении, уяснить его суть. Выработать навыки нахождения определенного интеграла, умения пользоваться свойствами и методами интегрирования.
2. Развивающая: Развивать математически грамотную речь, внимание, память, сознательное восприятие учебного материала.
3. Воспитательная: Воспитывать познавательную активность, сообразительность и мышление, благодарность к достижению великих математиков в области интегрирования.
Литература:
1. Математика: учебное пособие для техникумов. В.Т.Лисичкин, И.Л.Соловейчик, М., «Высшая школа», 1991г.
2. Практические занятия по математике: учебное пособие для техникумов. Н.В.Богомолов, М., «Высшая школа», 1990г.
3. Справочник по математике для средних учебных заведений А.Г.Цыпкин, М., «Наука», 1988г.
4. Математика для техникумов И.И.Валуцэ, Г.Д.Дилигул, М., «Наука», 1990г.
5. Задачник по высшей математике А.Т.Рогов, М., «Высшая школа», 1973г.
Лекция “Геометрический смысл определенного интеграла. Свойства. Методы вычисления.”
1.Определение и свойства определенного интеграла. Формула Ньютона – Лейбница.
Построение понятия определенного интеграла состоит из следующих этапов.
Пусть на отрезке [a, b] определена функция у = f(x). Отрезок [a, b] разобьем на п частей точками а = х0 < х1 < х2 < ….. < х < хп = b (разбиение R). На любом отрезке( 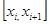 - частичный отрезок) выберем по произвольной точке ξ
- частичный отрезок) выберем по произвольной точке ξ 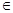 [х
[х 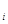 , xi+1]. (Рис1) ∆х
, xi+1]. (Рис1) ∆х 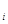 =х
=х 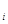 +1-х
+1-х 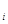 - длина отрезка. Составим сумму S
- длина отрезка. Составим сумму S 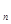 =
= 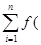 ξ
ξ 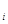 )∆х
)∆х  - n – ая интегральная сумма (Римана) функции f на отрезке [a, b].
- n – ая интегральная сумма (Римана) функции f на отрезке [a, b].
 Геометрический смысл суммы Sn - это есть алгебраическая сумма площадей
Геометрический смысл суммы Sn - это есть алгебраическая сумма площадей
прямоугольников, в основании которых лежат отрезки ∆x  , a
, a
высоты равны f(ξ 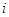 ). (В том
). (В том
случае функция неотрицательна функция)
Обозначим через γR = max ∆x 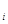 - максимальную длину отрезков
- максимальную длину отрезков
длину отрезков [х 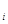 х
х 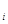 +1] разбиения R. Предел (если он существует), к которому стремится интегральная сумма рис1. Sn, когда γR = max ∆x
+1] разбиения R. Предел (если он существует), к которому стремится интегральная сумма рис1. Sn, когда γR = max ∆x 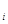 →0, называется определенным интегралом от функции f на отрезке [a, b] и обозначается:
→0, называется определенным интегралом от функции f на отрезке [a, b] и обозначается:
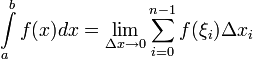 |
(1)
Предел (1) называют интегралом Римана и функцию, для которой этот предел существует называют интегрируемой в смысле Римана.
Определение:Определенным интегралом функции у= 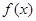 на отрезке
на отрезке 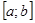 называется интеграл:
называется интеграл: 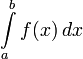
a – нижний предел.
b – верхний предел.
f(x) – подынтегральная функция.
dx- дифференциал независимой переменной.
Непосредственное вычисление определенного интеграла по формуле (1) связано с рядом трудностей, так как интегральные суммы имеют сложный вид, и найти их предел нелегко. До XVII века вычисление интегралов являлось трудной математической задачей. Ньютон и Лейбниц указали метод решения таких задач путем сведения к отысканию первообразной функции.
Таким образом, определенный интеграл вычисляется с помощью фундаментальной формулы Ньютона – Лейбница:
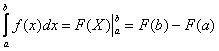 |
Определенный интеграл обладает рядом свойств, аналогичных свойствам неопределенного интеграла:
1) Постоянный множитель можно выносить за знак интеграла :
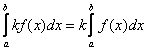 |
Интеграл от алгебраической суммы равен сумме интегралов от этих функций:
2) Для любых чисел a, b и с имеет место равенство:
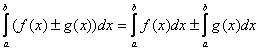 | ||
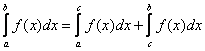 | ||
4) При перемене местами пределов интегрирования интеграл изменяет лишь знак:
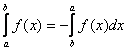
5) 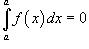
2. Вычисление определенных интегралов различными методами.
1. Непосредственное интегрирование - вычисление интегралов с помощью
непосредственного использования таблицы простейших интегралов, основных свойств
неопределенных интегралов и формулы Ньютона – Лейбница.
2. Замена переменной в определенном интеграле:
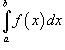 |
Определенный интеграл
по переменной x можно преобразовать в определенный интеграл относительно переменной
t с помощью подстановки x = g (t):
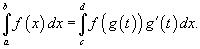
Новые пределы интегрирования по переменной t определяются выражениями
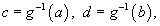 |
где g 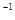 - обратная функция к g, т.е. t = g
- обратная функция к g, т.е. t = g 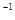 (x).
(x).
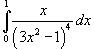 |
Пример1:
Решение.
Сделаем замену:
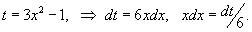
Пересчитаем пределы интегрирования. Если x = 0, то t = −1. Если же x = 1, то
t = 2. Тогда интеграл через новую переменную t легко вычисляется:
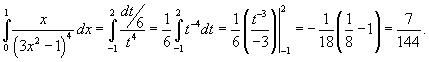 |
3. Интегрирование по частям для определенного интеграла
В этом случае формула интегрирования по частям имеет вид:
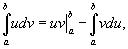 |
Где u и v – непрерывно дифференцируемые функции от х. С помощью этой формулы
нахождение интеграла 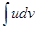 сводится к отысканию другого интеграла
сводится к отысканию другого интеграла 
При этом за u берется такая функция, которая при дифференцировании упрощается,
за dv – та часть подынтегрального выражения, интеграл от которой известен или
может быть найден.
Пример 2:
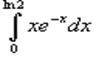 |
Вычислить интеграл
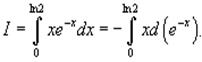 |
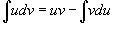 Используем интегрирование по частям: В нашем случае пусть будет
Используем интегрирование по частям: В нашем случае пусть будет
 |
Следовательно, интеграл равен
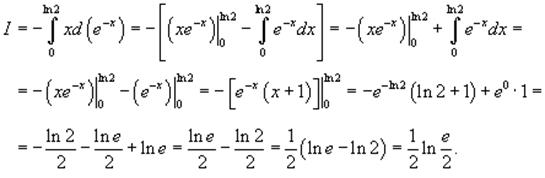 |
3. Применение определенного интеграла к вычислению площади плоской фигуры,
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|