Хелпикс

Главная

Контакты

Случайная статья



Задачи для самостоятельной работы

⇐ ПредыдущаяСтр 2 из 2


Задачи для самостоятельной работы

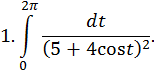
Ответ: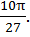
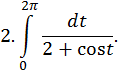
Ответ: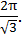
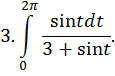
Ответ: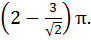

2.Вычисление несобственных интегралов с помощью вычетов

Еще больший интерес представляет возможность применения вычетов для вычисления несобственных интегралов

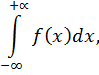
где интеграл понимается в смысле главного значения, то есть

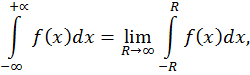
(здесь отрезок ).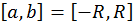

Будем рассматривать функцию 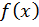, непрерывную на . Возможность использования вычетов при решении такой задачи основана на том, что отрезок  действительной оси рассматривается как часть замкнутого контура C, состоящего из этого отрезка и дуги окружности, а интеграл по контуру записывается в виде суммы:

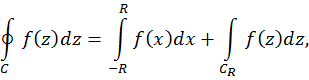
где 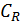 – дуга окружности

Несобственный интеграл определяется как предел

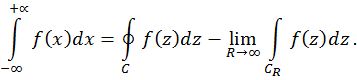
Интерес, с точки зрения применения вычетов, представляют интегралы

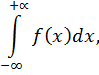
где функция 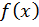 такова, что

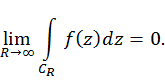
Классы таких функций выделяются, и для всех функций рассматриваемого класса устанавливается формула

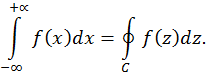
Интегралы вида

Здесь 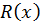– рациональная функция переменной x.

Теорема.

Пусть 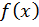- рациональная функция вида  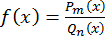, где  ,  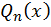–многочлены степеней m и n соответственно. Если  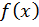–непрерывна на всей действительной оси и  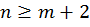, то

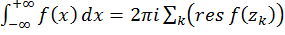   , где 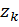 – полюса , расположенные в верхней полуплоскости.

Пример 3. Вычислить несобственный интеграл, используя вычеты.

 

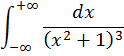
Решение.  Введем функцию 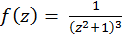 ; имеет в верхней полуплоскости особую точку 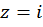 – полюс 3-го порядка.

 

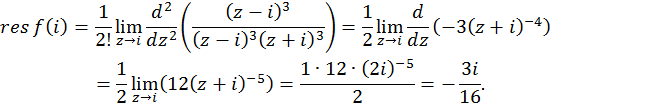
Тогда
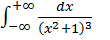 = 2  .

 

 


⇐ Предыдущая12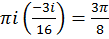
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.